Assignment 3

Introduction

Tidal wave propagation over long channels is a fundamental phenomenon in rivers and estuaries around the world. The flow velocity induced by the flood and ebb can have a detriment effect on navigation. These same flow velocities influence morphological time scales as well as water quality. The water level amplitudes along the channel influences flood risk calculations. In fact, the methods of the present assignment were developed and used by a committee headed by H.A. Lorentz to ensure that the closure of the Zuiderzee would not have detrimental effects on the rest of the Wadden sea coast. The following footage captures the situation before the construction.

Question 1

A tide propagating over a very long channel is a progressive/propagating wave that can be represented as a harmonic wave \(\zeta(s,t)=\overline{\zeta}(s)\cos{(\omega t-ks+\alpha)}\), where \(\omega\) is the frequency, \(k\) the (real-valued) wave number and \(\alpha\) the initial phase. \(\overline{\zeta}(s)\) is the surface perturbation amplitude that varies spatially along the channel.

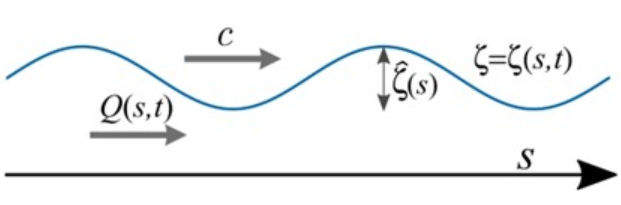
Fig. 10 Figure1

Consider a progressive wave in a 7-m depth channel with an amplitude \(\overline{\zeta}(s=0)=1.1\,\mathrm{m}\), an initial phase \(\alpha=0\,\mathrm{rad}\) and a length \(L=200\,\mathrm{km}\). In absence of damping/resistance the amplitude remains constant along the channel.

Model answer

\[ \zeta(s=100\,\mathrm{km},t=0\,\mathrm{s})=\overline{\zeta}(s)\cos{(\omega t-ks+\alpha)}=-1.1\,\mathrm{m} \]

Here, \(k=\frac{2\pi}{L}\)

Question 2

Model answer

The water level \(h\) equals the mean level (constant in time and space) plus the perturbation \(\zeta\).

\[ h(s=100\,\mathrm{km},t=0\,\mathrm{s})=h_0+\zeta(s=100\,\mathrm{km},t=0\,\mathrm{s})=7-1.1=5.9\,\mathrm{m} \]

Question 3

Model answer

The length of a periodic wave in radians is \(2\pi\), which means that the distance between the maximum and minimum values is half of the wave length: \(\pi\).

Question 4

Model answer

Apply logarithmus:

\[ \mu=-\frac{\ln{\frac{\overline{\zeta}(s)}{\overline{\zeta}(0)}}}{s} \]

Question 5

Model answer

Have a look at the unit. The exponent has to be non-dimensional. Therefore the units of \(\mu\) need to be the inverse ones of \(s\).

Question 6

The surface perturbation can be expressed as the real part of a complex expression: \(\zeta(s,t)=\overline{\zeta}(0)e^{-\mu s}\cos{(\omega t-ks+\alpha)}=\operatorname{Re}\left(\overline{\zeta}(0)e^{-\mu s}e^{i(\omega t-ks+\alpha)}\right)\) which can be divided in space and time components: \(\zeta(s,t)=\operatorname{Re}\left(\overline{\zeta}(0)e^{-\mu s+i(-ks+\alpha)}e^{i\omega t}\right)=\operatorname{Re}\left(\overline{\zeta}(s)e^{i\omega t}\right)\) where \(\overline{\zeta}(s)\) is the complex amplitude.

Model answer

The complex amplitude has a real and imaginary part, its length represents the amplitude \(\overline{\zeta}(s)\) and its angle represents the phase.

Question 7

A hodograph is a graphical representation in the complex plane of the complex ampitude \(\tilde{\zeta}(s)=\hat{\zeta}(0)e^{-\mu s+i(-ks+\alpha)}=\tilde{\zeta}(0)e^{-(\mu+ik)s}\)

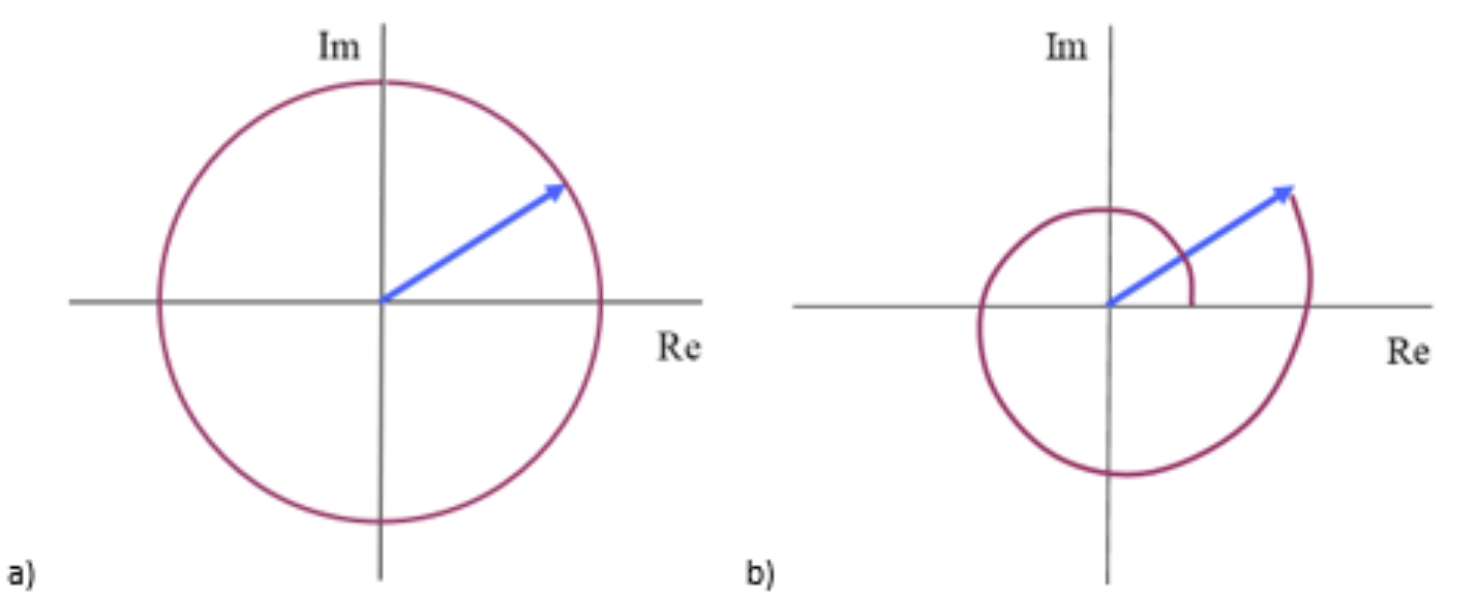
Model answer

The length of the complex amplitude vector of an hodograph characterized by a circle is constant at any phase, so it does not experience damping. The spiral exhibits damping behaviour.

Question 8

What is represented in the following hodograph?

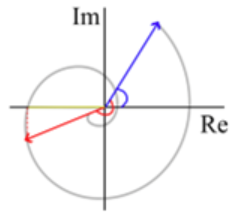
Model answer a

The largest length of a spiral (hodograph) in a progressive wave can only occur at the point where resistance has no effect (at \(s=0\)).

Model answer b

The amplitude is independent of time. The red line is smaller than the blue one, hinting that it has experienced damping and its location \(s\) is larger than \(0\).

Model answer c

The yellow vector is the projection of the red one on the real axis. In other words, it corresponds to the real component of the red vector, \(\zeta(s,t)=\operatorname{Re}\{\tilde{\zeta}(0)e^{-\mu s+i(-ks+\alpha)}e^{i(\omega t)}\}=\operatorname{Re}\{\tilde{\zeta}(s)e^{i(\omega t)}\}\). So, it represents the surface perturbation but the complex amplitude does not take into account time, which is equivalent as assuming \(t=0\)

Model answer d

Only the imaginary terms of the exponential \(\tilde{\zeta}(s)=\tilde{\zeta}(0)e^{-\mu s+i(-ks+\alpha)}\) can rotate the vector in the complex plane. The blue angle represents the angle of the blue vector, which is at \(s=0\). So \(ks=0\), the only other part that can shift it away from the pure real part is \(\alpha\).

Model answer e

The red angle \(\theta_3\) represents the angle between the blue and red vectors, with angles \(\theta_1=-ks+\alpha=\alpha\) and \(\theta_2=-ks+\alpha\) (with respect to the real axis). So the red angle is the difference between them \(\theta_3=\theta_1-\theta_2=\alpha-(-ks+\alpha)=ks\).

Question 9

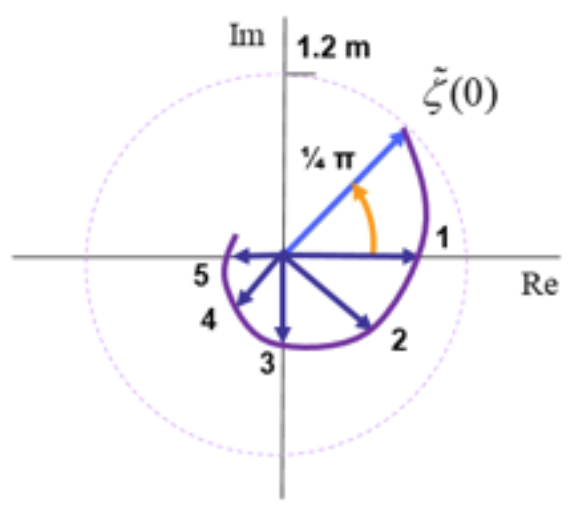
The following figure corresponds to \(t=0, \tilde{\zeta}(0)=(1.2\,\mathrm{m})e^{\frac{i\pi}{4}}​, k=\pi 10^{−5}\,\mathrm{rad/m}\) and damping parameter \(\mu=1\cdot 10^{-5}\,\mathrm{m^{-1}}\).

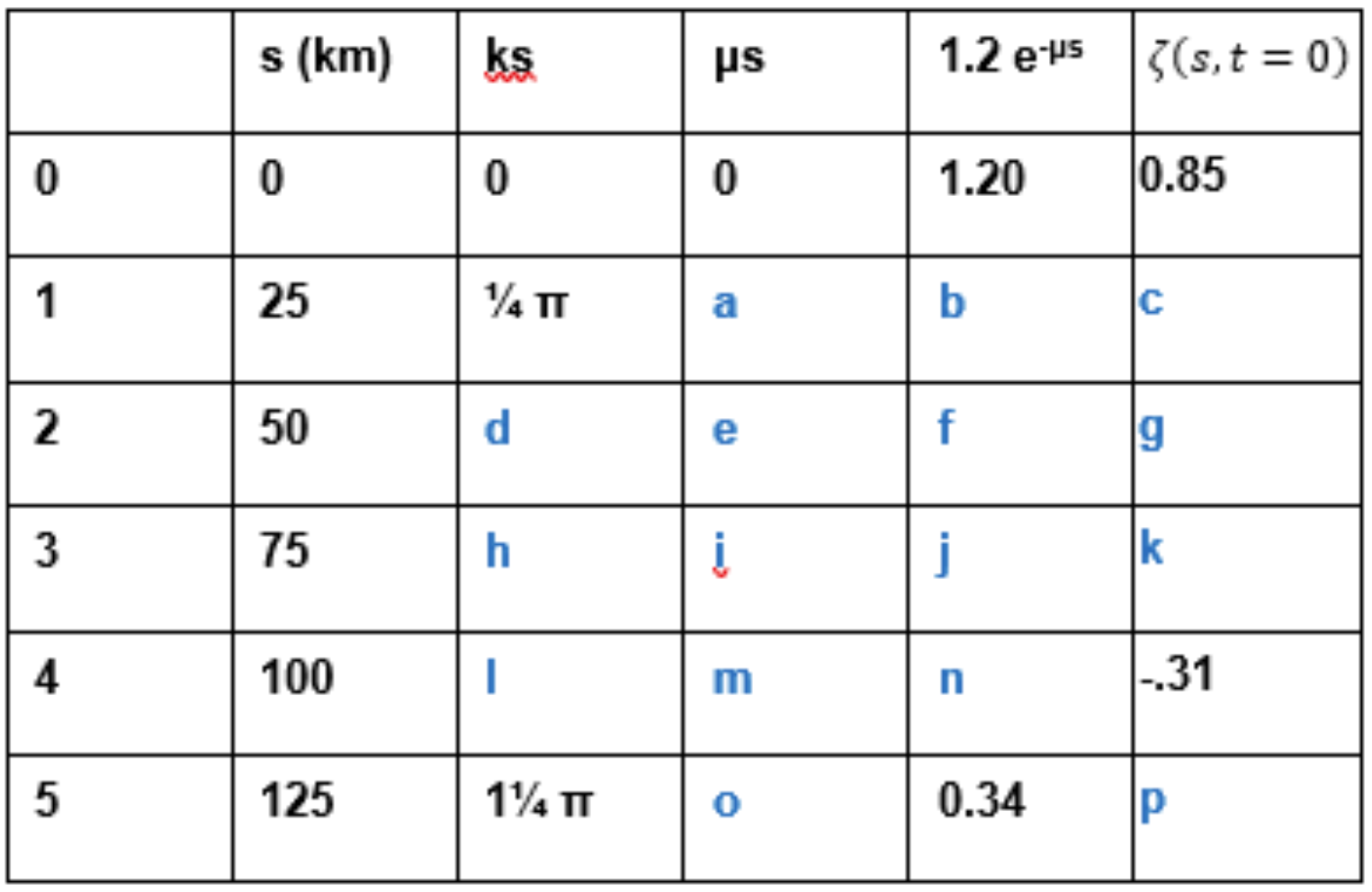
Question 10

Evaluate the relevance of each term of the general momentum equation for 1D long waves,

\[ \frac{\partial V}{\partial t}+\frac{\partial V^2}{\partial s}+g\frac{\partial h}{\partial s}+\frac{c_f|V|V}{h}=0 \]

for a typical situation of a tide propagating into an estuary. Consider an estuary with a depth of 20 m and a tide with a length of 600 km, wave height of 1 m, a period of 12h 25 min and a characteristic flow velocity of 0.6m/s, the resistance coefficient cf is equal to 0.004.

Select which statement described the importance of the term in this situation the best:

Model answer a

Let’s choose the resistance parameter to scale all the other ones respect to it. The ratio between the local acceleration and the resistance term equals 0.18. So, it cannot be neglected. See lecture 8 for a more complete description of terms estimation.

Model answer b

The ratio advective acceleration / resistance equals 0.008, so the advective term plays a small role in this situation (compared with the resistance) and can be neglected.

Model answer c

So far, the resistance term has been larger than the local and advective term. It is missing information to compare it with the gravity term. To determine the order of the gravity term it is missing the wave height value. A typical value would be 1m, in this case the ratio gravity/resistance equals 0.22. The resistance term is the most important one, and this would remain true even for wave heights of 4m. For this case, supposing that the flow velocity remains the same, the ratio gravity/resistance would equal 0.9.

Model answer d

Following the previous answer, the gravity term is lower than the resistance but it would still play an important role in this situation.

Question 11

For a tidal wave entering an estuary, river or channel, the second term of the momentum equation can be neglected, having as governing equations the following balances:

\[\begin{split} B\frac{\partial\zeta}{\partial t}+\frac{\partial Q}{\partial s}=0\\ \frac{\partial Q}{\partial t}+gA_c\frac{\partial\zeta}{\partial s}+c_f\frac{|Q|Q}{A_cR}=0 \end{split}\]

Note that \(h\) has been changed to \(\zeta\). This transformation is possible because \(h(s,t)=h_o+\zeta(s,t)\), where \(h_o\)​ is the mean water level and \(\zeta\) is the fluctuation around this value. The resistance term can be replaced by a linearized term:

\[ \frac{\partial Q}{\partial t}+gA_c\frac{\partial\zeta}{\partial s}+\Phi Q=0 \]

This principle states that the dissipation by the linearized friction term during a tidal cycle should be equal to the dissipation by the original quadratic friction during a tidal cycle:

\[ \Phi=\frac{8}{3\pi}c_f\frac{\hat{Q}}{A_cR} \]

Be aware that \(\hat{Q}\) is in fact a guess of the maximum discharge expected and will be assumed as a known value. However, rigorously speaking, the value of \(\hat{Q}\)​ should be iterated until reaching convergence.

Model answer

The derivative of the continuity equation respect to time is \(B\frac{\partial}{\partial t}\frac{\partial\zeta}{\partial t}+\frac{\partial}{\partial t}\frac{\partial Q}{\partial s}=0\,(15.1)\) and the derivative of the momentum equation with respect to space is \(\frac{\partial}{\partial s}\frac{\partial Q}{\partial t}+gA_c\frac{\partial}{\partial s}\frac{\partial\zeta}{\partial s}+\Psi\frac{\partial}{\partial s}Q=0\,(15.2)\). The third term of 15.2 can be rewritten using the continuity equation \(\frac{\partial Q}{\partial s}=-B\frac{\partial\zeta}{\partial t}\). So \(\frac{\partial}{\partial s}\frac{\partial Q}{\partial t}+gA_c\frac{\partial}{\partial s}\frac{\partial\zeta}{\partial s}-B\Psi\frac{\partial\zeta}{\partial t}=0\,(15.3)\).

And both equations can be combined by substracting 15.3 from 15.1:

\(B\frac{\partial^2\zeta}{\partial t^2}-gA_c\frac{\partial^2\zeta}{\partial s^2}+B\Psi\frac{\partial\zeta}{\partial t}=0\). Finally the result is obtained by dividing it by the storage width.

Question 12

The tidal wave motion can be treated as in part 1 of this assignment, as the real part of a complex quantity \(\zeta(s,t)=\operatorname{Re}\{\tilde{\zeta}(s)e^{i(\omega t)}\}\). Substitute \(\sqrt{\frac{gA_c}{B}}=c_0\)​​ (being the phase (and wave) velocity in the absence of resistance) and apply \(\zeta(s,t)=\operatorname{Re}\{\tilde{\zeta}(s)e^{i(\omega t)}\}\) to the Telegraph equation to obtain the reduced Telegraph equation. Hint: the time dependence drops after deriving \(\zeta\).

Model answer

The blue term in the previous answer is \(\frac{gA_c}{B}=c_0^2\). Substitute \(\zeta(s,t)=\operatorname{Re}\{\tilde{\zeta}(s)e^{i(\omega t)}\}\) on the telegrapgh equation and only apply the time derivatives, resulting in \(\frac{\partial\zeta}{\partial t}=\operatorname{Re}\{i\omega\tilde{\zeta}(s)e^{i(\omega t)}\}\) and \(\frac{\partial^2\zeta}{\partial t^2}=\operatorname{Re}\{-\omega^2\tilde{\zeta}(s)e^{i(\omega t)}\}\). The telegraph equation yields \(\operatorname{Re}\{-\omega^2\tilde{\zeta}(s)e^{i(\omega t)}\}-c_0^2\frac{\partial^2\operatorname{Re}\{\tilde{\zeta}(s)e^{i(\omega t)}\}}{\partial s^2}+\Psi \operatorname{Re}\{i\omega\tilde{\zeta}(s)e^{i(\omega t)}\}=0\). The term \(e^{i(\omega t)}\) drops and the \(\operatorname{Re}\) can be ignored from the equation, remembering that we are dealing with a complex amplitude. The following step is to divide everything by \(-c_0^2\rightarrow\frac{\omega^2\tilde{\zeta}}{c_0^2}+\frac{\partial^2\tilde{\zeta}}{\partial s^2}-\frac{\Psi i\omega\tilde{\zeta}}{c_0^2}=0\). This equation can be slightly rewritten to obtain the answer shape.

Question 13

By defining a relative resistance \(\sigma=\frac{\Phi}{\omega}\) and using the wave number of the undamped system instead of the corresponding phase velocity, \(k_0=\frac{\omega}{c_0}\), the equation can be rewritten:

Model answer

\[ \frac{\partial^2\tilde{\zeta}}{\partial s^2}+k_0^2\left(1-i\sigma\right)\tilde{\zeta}=0 \]

Substitute \(\sigma=\frac{\Phi}{\omega}\) and \(k_0=\frac{\omega}{c_0}\) on the previous answer to find the result.

Question 14

Model answer

Sigma becomes 0 when neglecting resistance \(\rightarrow\frac{\partial^2\tilde{\zeta}}{\partial s^2}+k_0^2\tilde{\zeta}=0\). The solutions of \(\tilde{\zeta}(s)=C_1e^{P_1s}+C_2e^{P_2s}\) can be treated independently. So substituting first \(C_1e^{P_1s}\) on the equation results in \(\frac{\partial^2C_1e^{P_1s}}{\partial s^2}+k_0^2C_1e^{P_1 s}=P_1^2C_1e^{P_1s}+k_0^2C_1e^{P_1s}=0\). The term \(C_1e^{P_1s}\) drops resulting in \(P_1=\sqrt{-k_0^2}\). The same result is reached for \(P_2=\sqrt{-k_0^2}\). The root mean square expression of a negative number has two opposite complex solutions.

The solution can be interpreted as two waves travelling in opposite directions \(\tilde{\zeta}(s)=C_1e^{−e\gammma s}+C_2e^{−e\gamma s}\), where \(\gamma=k_0\)​. The term \(C_1\)​ represents a wave travelling in the positive direction and the one of \(C_2\)​ represents a wave travelling in the negative direction.

Question 15

Model answer

The discharge \(Q(s,t)=\operatorname{Re}\{\tilde{Q}(s)e^{i(\omega t)}\}\) can be expressed similarly as the surface perturbation \(\zeta (s,t)=\operatorname{Re}\{\tilde{\zeta}(s)e^{i(\omega t)}\}\). After substituting the continuity equation \(B\frac{\partial\zeta}{\partial t}+\frac{\partial Q}{\partial s}=B\frac{\partial \operatorname{Re}\{\tilde{\zeta}(s)e^{i(\omega t)}\}}{\partial t}+\frac{\partial \operatorname{Re}\{\tilde{Q}(s)e^{i(\omega t)}\}}{\partial s}=0 and deriving over time and dropping the time exponential (and the real notation) \)\rightarrow\frac{\partial\tilde{Q}}{\partial s}=-iB\omega\tilde{\zeta}=-iB\omega(C_1e^{-i\gamma s}+C_2e^{i\gamma s}). The integral of the complex discharge respect to s \(\rightarrow\tilde{Q}(s)=-i\omega B\left(\frac{C_1e^{-i\gamma s}}{-i\gamma}+\frac{C_2e^{i\gamma s}}{i\gamma}\right)\), this can be simplified to \(\tilde{Q}(s)=\frac{\omega B}{\gamma}\left(C_1e^{-i\gamma s}-C_2e^{i\gamma s}\right)\), where \(\gamma=k_0=\frac{\omega}{c_0}\) and the answer is obtained.

Question 16

Model answer

The solution procedure is similar to question 18 but sigma is not \(0\). The solutions of \(\tilde{\zeta}(s)=C_1e^{P_1s}+C_2e^{P_2s}\) can be treated independently. So substituting first \(C_1e^{P_1s}\) on the equation results in \(\frac{\partial^2C_1e^{P_1s}}{\partial s^2}+k_0^2(1-i\sigma)C_1e^{P_1s}=P_1^2C_1e^{P_1s}+k_0^2(1-i\sigma)C_1e^{P_1s}=0\), the term \(C_1e^{P_1s} drops resulting in \)P_1=\sqrt{-k_0^2(1-i\sigma)}\(. The same result is reached for \)P_2=\sqrt{-k_0^2(1-i\sigma)}\(. The root mean square expression of a negative number has two opposite complex solutions \)P_{1,2}=\mp ik_0\cdot\sqrt{1-i\sigma}=\mp i\gamma\(. Now \)\gamma=k_0\cdot\sqrt{1-i\sigma}$ has a real and an imaginary part.

Question 17

The result from the previous question can be related to the complex amplitude defined in part 1, where the resistance and the wave number (taking into account resistance) are explicitly defined: \(\tilde{\zeta}(s)=\tilde{\zeta}(0)e^{-(\mu+ik)s}=C_1e^{-i\gamma s}\). Note that \(C_1\) can be inferred by \(s=0\). Therefore, \(C_1=\tilde{\zeta}(0)=|\tilde{\zeta}(0)|e^{i\alpha}\) and \(−i\gamma s=−(\mu+ik)s\).

Model answer

Note from the previous paragraph that \(-i\gamma=-(\mu+ik)\) and multiply both sides by the imaginary number results in \(\gamma=-i\mu+k\).

Question 18

Apply the solution of \(\tilde{\zeta}(s)=C_1e^{-i\gamma s}+C_2e^{-i\gamma s}\) to the continuity equation to obtain the complex discharge:

Model answer

The discharge \(Q(s,t)=\operatorname{Re}\{\tilde{Q}(s)e^{i(\omega t)}\}\) can be expressed similarly as the surface perturbation \(\zeta (s,t)=\operatorname{Re}\{\tilde{\zeta}(s)e^{i(\omega t)}\}\). After substituting the continuity equation \(B\frac{\partial\zeta}{\partial t}+\frac{\partial Q}{\partial s}=B\frac{\partial \operatorname{Re}\{\tilde{\zeta}(s)e^{i(\omega t)}\}}{\partial t}+\frac{\partial \operatorname{Re}\{\tilde{Q}(s)e^{i(\omega t)}\}}{\partial s}=0 and deriving over time and dropping the time exponential (and the real notation) \)\rightarrow\frac{\partial\tilde{Q}}{\partial s}=-iB\omega\tilde{\zeta}=-iB\omega(C_1e^{-i\gamma s}+C_2e^{i\gamma s}). The integral of the complex discharge respect to s \(\rightarrow\tilde{Q}(s)=-i\omega B\left(\frac{C_1e^{-i\gamma s}}{-i\gamma}+\frac{C_2e^{i\gamma s}}{i\gamma}\right)\), this can be simplified to \(\tilde{Q}(s)=\frac{B\omega}{\gamma}\left(C_1e^{-i\gamma s}-C_2e^{i\gamma s}\right)\).

Question 19

The propagation of the tide on a very long river behaves as a damped progressive wave. In other words, the tide decays as it propagates, and there is no leftward propagating wave because of the absence of a boundary at the right side, so \(C_2=0\). In other words, the river is infinite and therefore the “radiation condition” applies.

In \(s=0\) the amplitude of the tide at the entrance is \(0.85\,\rm{m}\) and its phase is \(\frac{π}{6}\), \(\tilde{\zeta}(s=0)=0.85e^{\frac{i\pi}{6}}\). The storage width is \(B=400\,\rm{m}\), conveyance area \(A_c=3600\,\rm{m^2}\) and hydraulic radius is \(R=12\,\rm{m}\). The tide has a period T of \(12\) hours and \(25\) minutes. Assume a friction coefficient \(c_f=0.0004\) and flow amplitude \(\hat{V}=0.90\,\rm{m/s}\) (\(\Phi\) has to be computed).

Model answer

The solution of the complex surface of a progressive wave is \(\tilde{\zeta}(s)=C_1e^{P_1s}\) because there is no reflection, substituting \(s\) for \(0\) indicates that \(C_1=\tilde{\zeta}(s=0)=0.85e^{i\frac{\pi}{6}}\).

Question 20

Model answer

The phase velocity is the propagation velocity taking into account resistance. The frequency of the tide is not affected by the resistance, only the wave number. So the phase velocity is \(c_{ph}=\frac{\omega}{k}\), and from question 21 the result that \(k\) is the real part of \(\gamma\) was found. This can be computed directly using maple (or matlab or python). \(R=12;g=9.81;\omega=0.00014;A_c=3600;B=400;V=0.9;c_f=0.004;c_0=\sqrt{\frac{g\cdot A_c}{B}};\) \(k_0=\frac{\omega}{c_0};\Psi=\frac{8}{3\pi};c_f\frac{\hat{V}}{R};\sigma=\frac{\Psi}{\omega};\) \(\gamma=k_0\sqrt{1-i\sigma};c=\frac{\omega}{\operatorname{Re}\{\gamma\}}\)

Question 21

Model answer

We know from that \(\tilde{Q}(s)=\frac{\omega B}{\gamma}C_1e^{-i\gamma s}\) and from question 19 the value of \(C_1\). Note that \(e^{-i\gamma s}=1\). \(\tilde{Q}=0.85\frac{B\omega}{\gamma}e^{i\frac{\pi}{6}}\) \(\hat{Q}=|\tilde{Q}|\)

Question 22

Model answer

\(\tilde{\zeta}(s=0)=0.85e^{i\frac{\pi}{6}}\) at \(s=0\) the only existing angle is \(\frac{\pi}{6}\)

Question 23

Model answer

Visualizing the complex plane, the argument of \(\tilde{Q}(s=0)\) represents its initial phase. So, its computed using the argument of the complex amplitude.

Question 24