Lecture 4 exercise 1 cable

Lecture 4 exercise 1 cable#

%reset -f
import sympy as sp

L = sp.S(6)
a = sp.S(2)
b = sp.S(2)
c = L - a - b
q1 = sp.S(5)
q2 = sp.S(0)
q3 = sp.S(0)
F = sp.S(15)

Bv = (q1*a*a/2+F*(a+b))/(a+b+c)
display(Bv)
H = Bv*c*5/4
display(H)
display(H.evalf())

\[\displaystyle \frac{35}{3}\]

\[\displaystyle \frac{175}{6}\]

\[\displaystyle 29.1666666666667\]

H= sp.symbols('H',real=True,positive=True)
x = sp.symbols('x',real=True)
C1, C2, C3, C4, C5, C6 = sp.symbols('C1 C2 C3 C4 C5 C6')
z1, z2, z3 = sp.symbols('z1 z2 z3',cls=sp.Function)
ODE1 = sp.Eq(H * sp.diff(z1(x),x,2) , -q1)
ODE2 = sp.Eq(H * sp.diff(z2(x),x,2) , -q2)
ODE3 = sp.Eq(H * sp.diff(z3(x),x,2) , -q3)
sol = sp.dsolve([ODE1,ODE2,ODE3],[z1(x),z2(x),z3(x)])
z1 = sol[0].rhs
z2 = sol[1].rhs
z3 = sol[2].rhs

V1 = H * sp.diff(z1,x)
V2 = H * sp.diff(z2,x)
V3 = H * sp.diff(z3,x)

eq1 = sp.Eq(z1.subs(x,0),0)
eq2 = sp.Eq(z3.subs(x,L),0)
eq3 = sp.Eq(z1.subs(x,a),z2.subs(x,a))
eq4 = sp.Eq(V1.subs(x,a),V2.subs(x,b))
eq5 = sp.Eq(z2.subs(x,a+b),z3.subs(x,a+b))
eq6 = sp.Eq(V2.subs(x,a+b),V3.subs(x,a+b)+F)

sol = sp.solve([eq1,eq2,eq3,eq4,eq5,eq6],[C1,C2,C3,C4,C5,C6])
z1 = z1.subs(sol)
z2 = z2.subs(sol)
z3 = z3.subs(sol)
display(z1)
display(z2)
display(z3)

\[\displaystyle - \frac{5 x^{2}}{2 H} + \frac{40 x}{3 H}\]

\[\displaystyle \frac{10 x}{3 H} + \frac{10}{H}\]

\[\displaystyle - \frac{35 x}{3 H} + \frac{70}{H}\]

exact

ds1 = sp.sqrt(1+sp.diff(z1,x)**2)
ds2 = sp.sqrt(1+sp.diff(z2,x)**2)
ds3 = sp.sqrt(1+sp.diff(z3,x)**2)
print(ds1)
print(ds2)
print(ds3)

sqrt((-5*x/H + 40/(3*H))**2 + 1)
sqrt(1 + 100/(9*H**2))
sqrt(1 + 1225/(9*H**2))

Taylor option 1

# ds1 = 1 + sp.diff(z1,x)**2/2
# ds2 = 1 + sp.diff(z2,x)**2/2
# ds3 = 1 + sp.diff(z3,x)**2/2

Taylor option 2

#ds1 = 1 + sp.diff(z1,x)**2/2 - sp.diff(z1,x)**4/8
#ds2 = 1 + sp.diff(z2,x)**2/2 - sp.diff(z2,x)**4/8
#ds3 = 1 + sp.diff(z3,x)**2/2 - sp.diff(z3,x)**4/8
display(ds1)
display(ds2)
display(ds3)

\[\displaystyle \sqrt{\left(- \frac{5 x}{H} + \frac{40}{3 H}\right)^{2} + 1}\]

\[\displaystyle \sqrt{1 + \frac{100}{9 H^{2}}}\]

\[\displaystyle \sqrt{1 + \frac{1225}{9 H^{2}}}\]

Length of cable

ds1 = sp.nsimplify(ds1)
ds2 = sp.nsimplify(ds2)
ds3 = sp.nsimplify(ds3)

#LL = sp.integrate(ds1,(x,sp.S(0),a))+sp.integrate(ds2,(x,a,a+b))+sp.integrate(ds3,(x,a+b,L))
LL = sp.integrate(ds1.subs(H,sp.nsimplify(175/6)),(x,0,a))+sp.integrate(ds2.subs(H,sp.nsimplify(175/6)),(x,a,a+b))+sp.integrate(ds3.subs(H,sp.nsimplify(175/6)),(x,a+b,L))
display(LL)
display(LL.evalf())
eq7 = sp.Eq(sp.integrate(ds1,(x,0,a))+sp.integrate(ds2,(x,a,a+b))+sp.integrate(ds3,(x,a+b,L)),sp.nsimplify(6.2558)) #same issue as in Examples_Base_Structural_Engineering/Exact_length_parabolic_cable.ipynb
display(sp.simplify(eq7))
H_sol = sp.nsolve(eq7,H,30)
display(H_sol)
H_sol = sp.nsimplify(H_sol)
display(H_sol)
LL  = sp.integrate(ds1.subs(H,H_sol),(x,0,a))+sp.integrate(ds2.subs(H,H_sol),(x,a,a+b))+sp.integrate(ds3.subs(H,H_sol),(x,a+b,L))
display(LL.evalf())

\[\displaystyle - \frac{35 \operatorname{asinh}{\left(\frac{4}{35} \right)}}{12} + \frac{35 \operatorname{asinh}{\left(\frac{16}{35} \right)}}{12} + \frac{4 \sqrt{1481}}{105} + \frac{\sqrt{1241}}{21} + \frac{2 \sqrt{29}}{5}\]

\[\displaystyle 6.25580223961325\]

\[\displaystyle \frac{- 9 H^{2} \operatorname{asinh}{\left(\frac{10}{3 H} \right)} + 9 H^{2} \operatorname{asinh}{\left(\frac{40}{3 H} \right)} + 50 \sqrt{9 H^{2} + 100} + 60 \sqrt{9 H^{2} + 1225} + 40 \sqrt{9 H^{2} + 1600}}{90 H} = \frac{31279}{5000}\]

\[\displaystyle 29.1667985144668\]

\[\displaystyle \frac{72916996286167}{2500000000000}\]

\[\displaystyle 6.2558\]

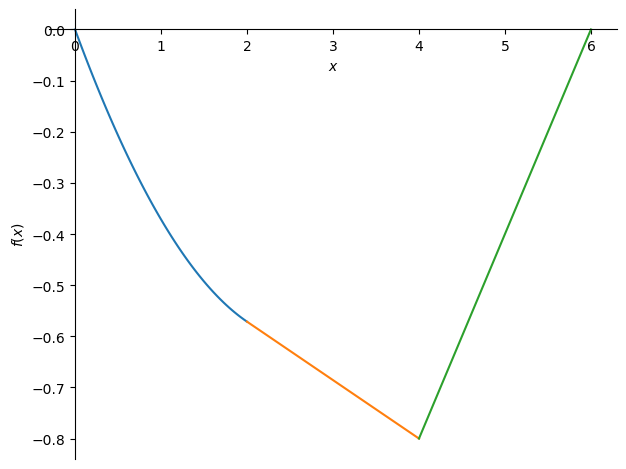
z1_sol = z1.subs(H,H_sol)
z2_sol = z2.subs(H,H_sol)
z3_sol = z3.subs(H,H_sol)
sp.plot((-z1_sol,(x,0,a)),(-z2_sol,(x,a,a+b)),(-z3_sol,(x,a+b,L)));

../_images/26c22da33c9ef824c678d0cac7f7c39bef841cce15152016d0d9fde467b08975.png

Alternative

%reset -f
import sympy as sp

L = sp.Integer(6)
a = sp.Integer(2)
b = sp.Integer(2)
c = L - a - b
F = sp.Integer(15)
q0 = sp.Integer(5)

H, x= sp.symbols('H x')
C1, C2 = sp.symbols('C1 C2')
z = sp.symbols('z',cls=sp.Function)

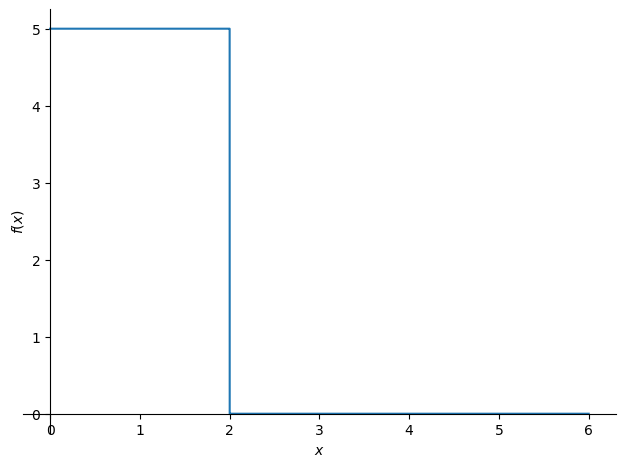
q = q0*(sp.Integer(1)-sp.Heaviside(x-a))+F*sp.DiracDelta(x-(a+b))
sp.plot(q,(x,0,L))

../_images/51fd696bb21acd5c6e72379927fa15bc5d408b1077244ee556c707313caacc80.png

<sympy.plotting.plot.Plot at 0x1d7dbba1f40>

V = sp.integrate(-q,x, meijerg=False)+C1
z = sp.integrate(V/H,x,  meijerg=False)+C2

display(V)
display(z)

eq1 = sp.Eq(z.subs(x,0),0)
eq2 = sp.Eq(z.subs(x,L),0)

sol = sp.solve([eq1,eq2,],[C1,C2])
z = z.subs(sol)

display(z)

\[\displaystyle C_{1} - 5 x + 5 \left(x - 2\right) \theta\left(x - 2\right) - 15 \theta\left(x - 4\right)\]

\[\displaystyle C_{2} + \frac{C_{1} x - \frac{5 x^{2}}{2} - 15 \left(x - 4\right) \theta\left(x - 4\right) + 5 \left(\frac{x^{2}}{2} - 2 x + 2\right) \theta\left(x - 2\right)}{H}\]

\[\displaystyle \frac{- \frac{5 x^{2}}{2} + \frac{40 x}{3} - 15 \left(x - 4\right) \theta\left(x - 4\right) + 5 \left(\frac{x^{2}}{2} - 2 x + 2\right) \theta\left(x - 2\right)}{H}\]

eq3 = sp.Eq(z.subs(x,a+b),4/5)
H_sol = sp.solve(eq3,H)[0]
H_sol = sp.nsimplify(H_sol)
display(H_sol)

\[\displaystyle \frac{175}{6}\]

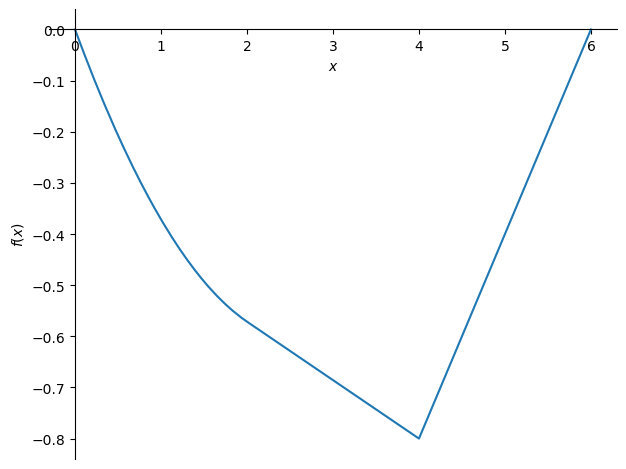
z_sol = z.subs(H,H_sol)
sp.plot(-z_sol,(x,0,L))

../_images/9be5119bb9ab6a81adb47a15e3e8b4a0e7cf31226462163a0c5bbc3b78d4aead.png

<sympy.plotting.plot.Plot at 0x1d7de3e1e20>

z_piecewise = z_sol.rewrite(sp.Piecewise) #direct gives wrong result, seems to do with https://github.com/sympy/sympy/issues/24274
LL = sp.integrate(sp.sqrt(1+sp.diff(z_piecewise,x)**2),(x,0,6))
display(LL)
display(LL.evalf())

\[\displaystyle - \frac{35 \operatorname{asinh}{\left(\frac{4}{35} \right)}}{12} + \frac{35 \operatorname{asinh}{\left(\frac{16}{35} \right)}}{12} + \frac{4 \sqrt{1481}}{105} + \frac{\sqrt{1241}}{21} + \frac{2 \sqrt{29}}{5}\]

\[\displaystyle 6.25580223961325\]