Sympy voorbeeld 2

import sympy as sp
x, C1, C2, C3, C4, C5, C6, C7, C8, q, F, EI, L1, L2 = sp.symbols('x C1 C2 C3 C4 C5 C6 C7 C8 q F EI L1 L2')

Definieer de verplaatsingen \(w_1\) en \(w_2\).

\(w_1\) voor \(0 < x < L_1\)

\(w_2\) voor \(L_1 < x < L_1+L_2\)

w1 = C1 * x**3 / 6 + C2 * x**2 / 2 + C3 * x + C4

w2 = q * x**4 / (24 * EI) + C5 * x**3 / 6 + C6 * x**2 / 2 + C7 * x + C8

Druk de verdraaiingen (\(\phi\)), de momenten (\(M\)) en de dwarskrachten (\(V\)) uit in \(w_1\) en \(w_2\).

\(\phi_1\), \(\kappa_1\), \(M_1\), \(V_1\) voor \(0 < x < L_1\)

\(\phi_2\), \(\kappa_2\), \(M_2\), \(V_2\) voor \(L_1 < x < L_1+L_2\)

phi1 = -w1.diff(x)
phi2 = -w2.diff(x)
kappa1 = phi1.diff(x)
kappa2 = phi2.diff(x)
M1 = EI * kappa1
M2 = EI * kappa2
V1 = M1.diff(x)
V2 = M2.diff(x)

Geef de rand- en overgangsvoorwaarden om de onbekenden (\(C_1\) t/m \(C_8\)) op te lossen. (8 onbekenden, dus 8 vergelijkingen nodig).

eq1 = sp.Eq(phi1.subs(x,0),0)
eq2 = sp.Eq(w1.subs(x,0),0)
eq3 = sp.Eq(w1.subs(x,L1),w2.subs(x,L1))
eq4 = sp.Eq(phi1.subs(x,L1),phi2.subs(x,L1))
eq5 = sp.Eq(M1.subs(x,L1),M2.subs(x,L1))
eq6 = sp.Eq(V1.subs(x,L1),V2.subs(x,L1)+F)
eq7 = sp.Eq(w2.subs(x,L1+L2),0)
eq8 = sp.Eq(M2.subs(x,L1+L2),0)

Laat Maple de 8 onbekenden oplossen met behulp van de 8 hierboven gegeven vergelijkingen.

sol = sp.solve((eq1,eq2,eq3,eq4,eq5,eq6,eq7,eq8),(C1,C2,C3,C4,C5,C6,C7,C8))
display(sol)
w1_sol = w1.subs(sol)
phi1_sol = phi1.subs(sol)
M1_sol = M1.subs(sol)
V1_sol = V1.subs(sol)
w2_sol = w2.subs(sol)
phi2_sol = phi2.subs(sol)
M2_sol = M2.subs(sol)
V2_sol = V2.subs(sol)

{C1: (-12*F*L1**2*L2 - 24*F*L1*L2**2 - 8*F*L2**3 - 6*L1**2*L2**2*q - 12*L1*L2**3*q - 5*L2**4*q)/(8*EI*L1**3 + 24*EI*L1**2*L2 + 24*EI*L1*L2**2 + 8*EI*L2**3),
 C2: (4*F*L1**2*L2 + 8*F*L1*L2**2 + 2*L1**2*L2**2*q + 4*L1*L2**3*q + L2**4*q)/(8*EI*L1**2 + 16*EI*L1*L2 + 8*EI*L2**2),
 C3: 0,
 C4: 0,
 C5: (8*F*L1**3 + 12*F*L1**2*L2 - 8*L1**4*q - 24*L1**3*L2*q - 30*L1**2*L2**2*q - 20*L1*L2**3*q - 5*L2**4*q)/(8*EI*L1**3 + 24*EI*L1**2*L2 + 24*EI*L1*L2**2 + 8*EI*L2**3),
 C6: (-8*F*L1**3 - 12*F*L1**2*L2 + 4*L1**4*q + 8*L1**3*L2*q + 6*L1**2*L2**2*q + 4*L1*L2**3*q + L2**4*q)/(8*EI*L1**2 + 16*EI*L1*L2 + 8*EI*L2**2),
 C7: (3*F*L1**2 - L1**3*q)/(6*EI),
 C8: (-4*F*L1**3 + L1**4*q)/(24*EI)}

w1_sub = w1_sol.subs([(F,20),(L1,3),(L2,5),(q,8),(EI,1000)])
phi1_sub = phi1_sol.subs([(F,20),(L1,3),(L2,5),(q,8),(EI,1000)])
M1_sub = M1_sol.subs([(F,20),(L1,3),(L2,5),(q,8),(EI,1000)])
V1_sub = V1_sol.subs([(F,20),(L1,3),(L2,5),(q,8),(EI,1000)])
w2_sub = w2_sol.subs([(F,20),(L1,3),(L2,5),(q,8),(EI,1000)])
phi2_sub = phi2_sol.subs([(F,20),(L1,3),(L2,5),(q,8),(EI,1000)])
M2_sub = M2_sol.subs([(F,20),(L1,3),(L2,5),(q,8),(EI,1000)])
V2_sub = V2_sol.subs([(F,20),(L1,3),(L2,5),(q,8),(EI,1000)])

Je kunt checken of het klopt. Zijn de zakkingen \(w_1\) en \(w_2\) nu hetzelfde op \(x = 3m\)? Ja! Je kunt natuurlijk alle andere rand- en overgangsvoorwaarden ook checken.

display(w1_sub.subs(x,3).evalf())
display(w2_sub.subs(x,3).evalf())

\[\displaystyle 0.1658935546875\]

\[\displaystyle 0.1658935546875\]

we kunnen de velden ook aan elkaar plakken, zodat je een gehele zakkings-, momenten- en dwarskrachtenlijn van de constructie krijgen.

w = sp.Piecewise((w1_sub,(x>=0) & (x<=3)),(w2_sub,(x>3)&(x<=8)))
phi = sp.Piecewise((phi1_sub,(x>=0) & (x<=3)),(phi2_sub,(x>3)&(x<=8)))
M = sp.Piecewise((M1_sub,(x>=0) & (x<=3)),(M2_sub,(x>3)&(x<=8)))
V = sp.Piecewise((V1_sub,(x>=0) & (x<=3)),(V2_sub,(x>3)&(x<=8)))
display(w)
display(phi)
display(M)
display(V)

\[\begin{split}\displaystyle \begin{cases} - \frac{231 x^{3}}{40960} + \frac{181 x^{2}}{5120} & \text{for}\: x \geq 0 \wedge x \leq 3 \\\frac{x^{4}}{3000} - \frac{19373 x^{3}}{3072000} + \frac{2989 x^{2}}{128000} + \frac{27 x}{500} - \frac{63}{1000} & \text{for}\: x \leq 8 \wedge x > 3 \end{cases}\end{split}\]

\[\begin{split}\displaystyle \begin{cases} \frac{693 x^{2}}{40960} - \frac{181 x}{2560} & \text{for}\: x \geq 0 \wedge x \leq 3 \\- \frac{x^{3}}{750} + \frac{19373 x^{2}}{1024000} - \frac{2989 x}{64000} - \frac{27}{500} & \text{for}\: x \leq 8 \wedge x > 3 \end{cases}\end{split}\]

\[\begin{split}\displaystyle \begin{cases} \frac{17325 x}{512} - \frac{4525}{64} & \text{for}\: x \geq 0 \wedge x \leq 3 \\- 4 x^{2} + \frac{19373 x}{512} - \frac{2989}{64} & \text{for}\: x \leq 8 \wedge x > 3 \end{cases}\end{split}\]

\[\begin{split}\displaystyle \begin{cases} \frac{17325}{512} & \text{for}\: x \geq 0 \wedge x \leq 3 \\\frac{19373}{512} - 8 x & \text{for}\: x \leq 8 \wedge x > 3 \end{cases}\end{split}\]

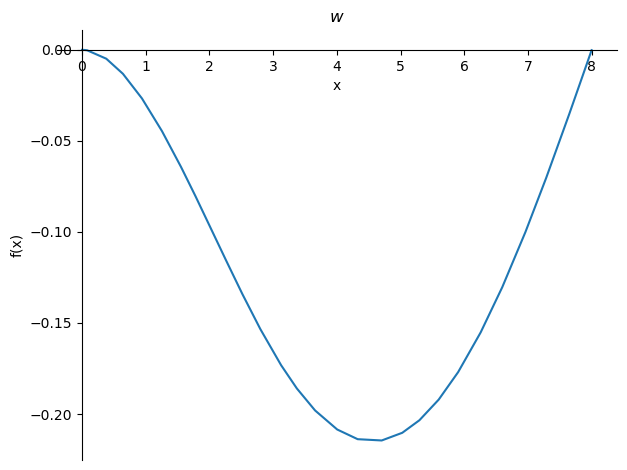
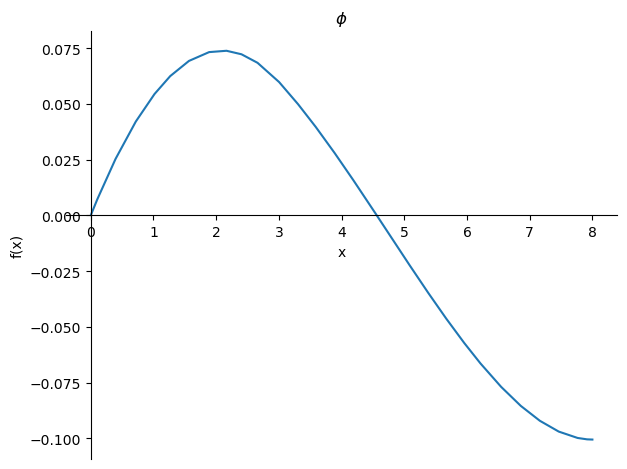
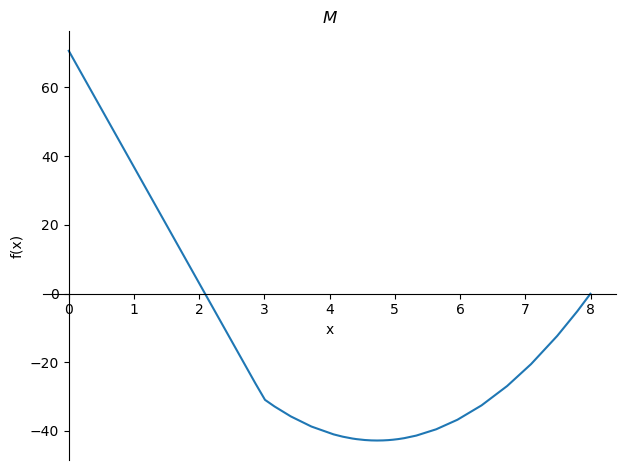
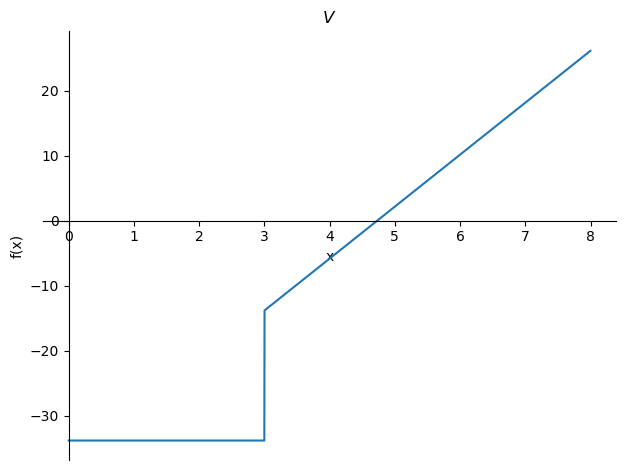
Ook kunnen we de lijnen \(w\), \(\phi\), \(V\) en \(M\) plotten in Python

sp.plot(-w,title='$w$');
sp.plot(-phi,title='$\phi$');
sp.plot(-M,title='$M$');
sp.plot(-V,title='$V$');