Singularity functions

Static determinate structure

M- and V-line

In this notebook, we’re solving beam equations using Macaulay’s method.

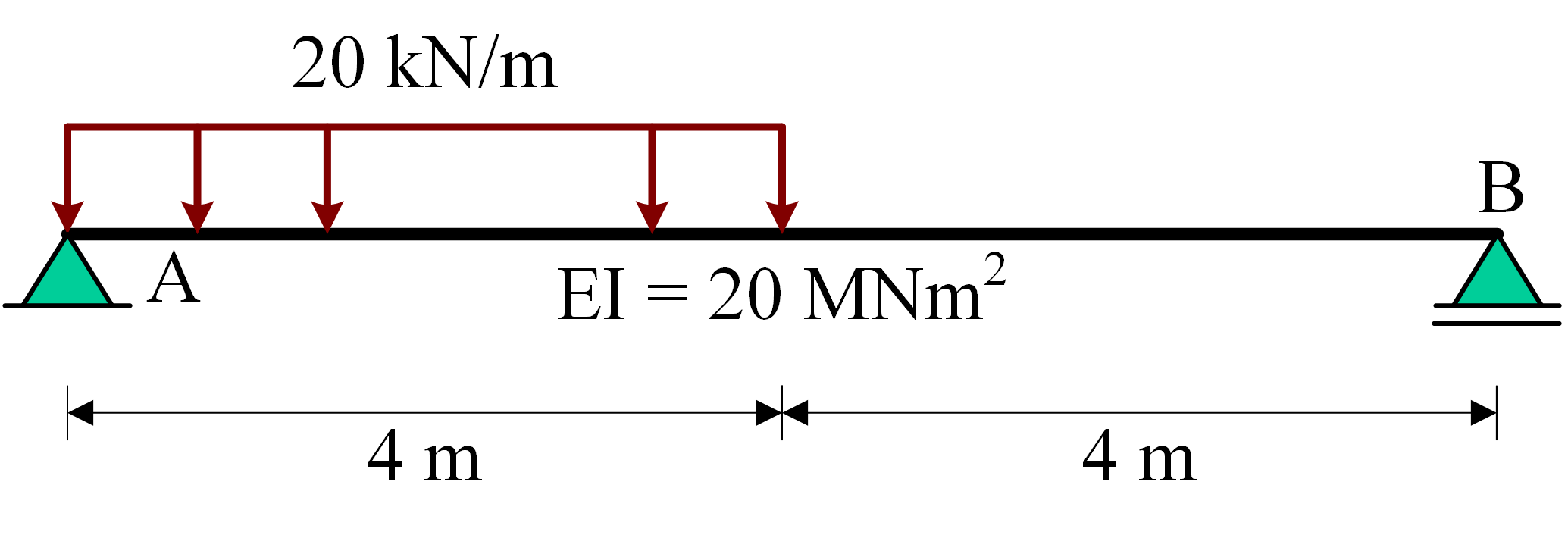
As this is a statically determinate structure, first the \(M\)- and \(V\)-line are solved for.

import sympy as sp

C1, C2, x, EI = sp.symbols('C1, C2, x, EI')
A_v, B_v = sp.symbols('A_v, B_v')
q0 = sp.symbols('q0')

The function \(q(x)\) is specified as a function of all external forces + support reactions

q = A_v * sp.SingularityFunction(x,0,-1) + q0 *sp.SingularityFunction(x,0,0) - q0*sp.SingularityFunction(x,4,0) + B_v * sp.SingularityFunction(x,8,-1)
display(q)

\[\displaystyle A_{v} {\left\langle x \right\rangle}^{-1} + B_{v} {\left\langle x - 8 \right\rangle}^{-1} + q_{0} {\left\langle x \right\rangle}^{0} - q_{0} {\left\langle x - 4 \right\rangle}^{0}\]

The functions \(V_1(x)\) and \(M_1(x)\) are calculated as integrals of \(q(x)\). These represent the sum of vertical and sum of moments up to a position \(x\).

V1 = -sp.integrate(q,x)
display(V1)
M1 = sp.integrate(V1,x)
display(M1)

\[\displaystyle - A_{v} {\left\langle x \right\rangle}^{0} - B_{v} {\left\langle x - 8 \right\rangle}^{0} - q_{0} {\left\langle x \right\rangle}^{1} + q_{0} {\left\langle x - 4 \right\rangle}^{1}\]

\[\displaystyle - A_{v} {\left\langle x \right\rangle}^{1} - B_{v} {\left\langle x - 8 \right\rangle}^{1} - \frac{q_{0} {\left\langle x \right\rangle}^{2}}{2} + \frac{q_{0} {\left\langle x - 4 \right\rangle}^{2}}{2}\]

Now the force and moment equilibria can be specified by substituting \(x=8\) for the equilibrium of the whole structure.

eq1 = sp.Eq(V1.subs(x,8),0)
eq2 = sp.Eq(M1.subs(x,8),0)
display(eq1)
display(eq2)

\[\displaystyle - A_{v} - B_{v} - 4 q_{0} = 0\]

\[\displaystyle - 8 A_{v} - 24 q_{0} = 0\]

The three unknown support reactions can now be solved

sol = sp.solve((eq1,eq2),(A_v,B_v))
display(sol)

{A_v: -3*q0, B_v: -q0}

The \(M-\) and \(V-\)lines can now be found by subsituting our support reactions. The result with singularity-functions can rewritten as a piecewise function aswell, which clearly shows a valid result.

M_sol = M1.subs(sol)
display(M_sol)
display(sp.simplify(M_sol.rewrite(sp.Piecewise)))
V_sol = V1.subs(sol)
display(V_sol)
display(sp.simplify(V_sol.rewrite(sp.Piecewise)))

\[\displaystyle 3 q_{0} {\left\langle x \right\rangle}^{1} - \frac{q_{0} {\left\langle x \right\rangle}^{2}}{2} + \frac{q_{0} {\left\langle x - 4 \right\rangle}^{2}}{2} + q_{0} {\left\langle x - 8 \right\rangle}^{1}\]

\[\begin{split}\displaystyle \begin{cases} 0 & \text{for}\: x > 8 \\q_{0} \cdot \left(8 - x\right) & \text{for}\: x > 4 \\\frac{q_{0} x \left(6 - x\right)}{2} & \text{for}\: x > 0 \\0 & \text{otherwise} \end{cases}\end{split}\]

\[\displaystyle 3 q_{0} {\left\langle x \right\rangle}^{0} - q_{0} {\left\langle x \right\rangle}^{1} + q_{0} {\left\langle x - 4 \right\rangle}^{1} + q_{0} {\left\langle x - 8 \right\rangle}^{0}\]

\[\begin{split}\displaystyle \begin{cases} 0 & \text{for}\: x > 8 \\- q_{0} & \text{for}\: x > 4 \\q_{0} \cdot \left(3 - x\right) & \text{for}\: x > 0 \\0 & \text{otherwise} \end{cases}\end{split}\]

M_subs = M_sol.subs(q0,20)
display(M_subs)
display(sp.simplify(M_subs.rewrite(sp.Piecewise)))
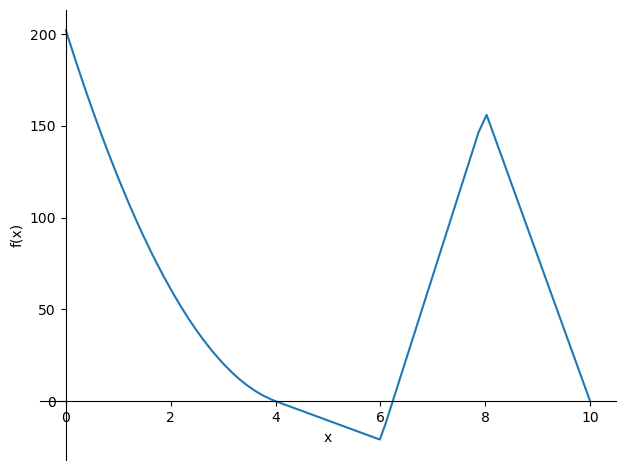
sp.plot(-M_subs,(x,0,8))
V_subs = V_sol.subs(q0,20)
display(V_subs)
display(sp.simplify(V_subs.rewrite(sp.Piecewise)))
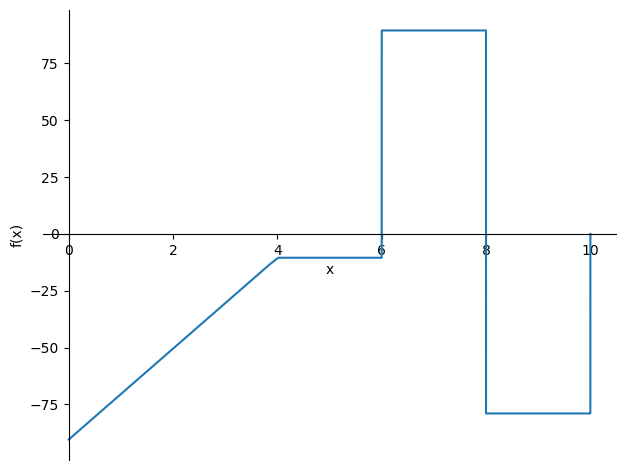
sp.plot(-V_subs,(x,0,8));

\[\displaystyle 60 {\left\langle x \right\rangle}^{1} - 10 {\left\langle x \right\rangle}^{2} + 10 {\left\langle x - 4 \right\rangle}^{2} + 20 {\left\langle x - 8 \right\rangle}^{1}\]

\[\begin{split}\displaystyle \begin{cases} 0 & \text{for}\: x > 8 \\160 - 20 x & \text{for}\: x > 4 \\10 x \left(6 - x\right) & \text{for}\: x > 0 \\0 & \text{otherwise} \end{cases}\end{split}\]

\[\displaystyle 60 {\left\langle x \right\rangle}^{0} - 20 {\left\langle x \right\rangle}^{1} + 20 {\left\langle x - 4 \right\rangle}^{1} + 20 {\left\langle x - 8 \right\rangle}^{0}\]

\[\begin{split}\displaystyle \begin{cases} 0 & \text{for}\: x > 8 \\-20 & \text{for}\: x > 4 \\60 - 20 x & \text{for}\: x > 0 \\0 & \text{otherwise} \end{cases}\end{split}\]

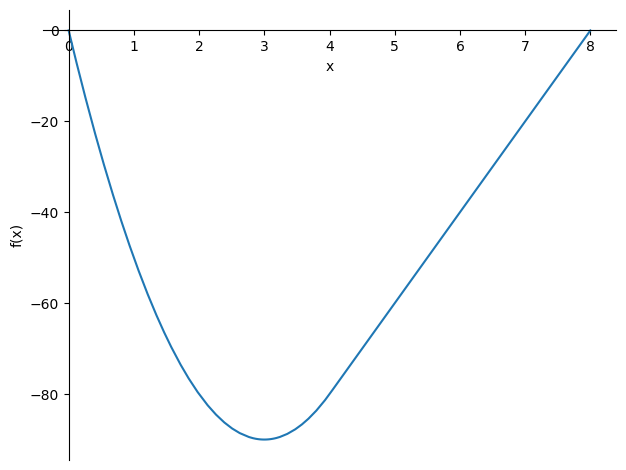
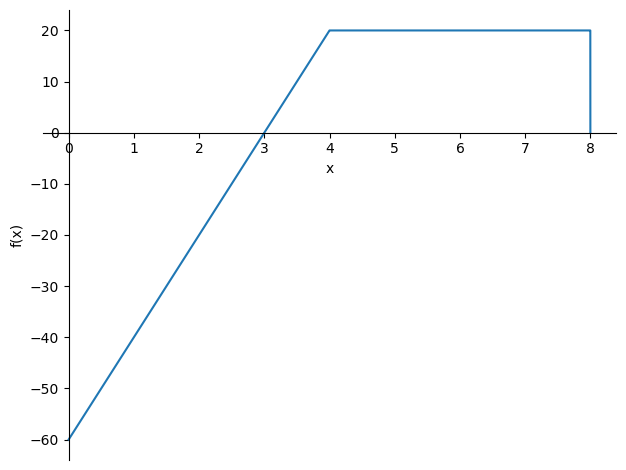
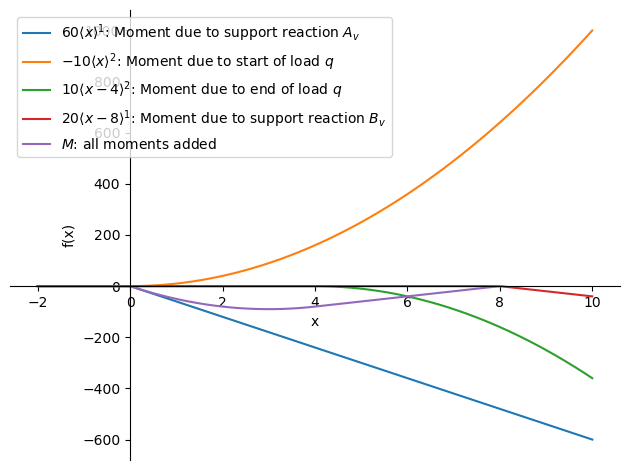
The influence of the support reactions and load can be splitted:

p0 = sp.plotting.plot(-M_subs.args[3],(x,-2,10),label='$'+sp.latex(M_subs.args[3])+'$'+": Moment due to support reaction $A_v$",legend=True,show=False)
p1 = sp.plotting.plot(-M_subs.args[0],(x,-2,10),label='$'+sp.latex(M_subs.args[0])+'$'+": Moment due to start of load $q$",show=False)
p2 = sp.plotting.plot(-M_subs.args[1],(x,-2,10),label='$'+sp.latex(M_subs.args[1])+'$'+": Moment due to end of load $q$",show=False)
p3 = sp.plotting.plot(-M_subs.args[2],(x,-2,10),label='$'+sp.latex(M_subs.args[2])+'$'+": Moment due to support reaction $B_v$",show=False)
p4 = sp.plotting.plot(-M_subs,(x,0,8),label='$M$: all moments added',show=False)
p0.append(p1[0])
p0.append(p2[0])
p0.append(p3[0])
p0.append(p4[0])
p0.show()

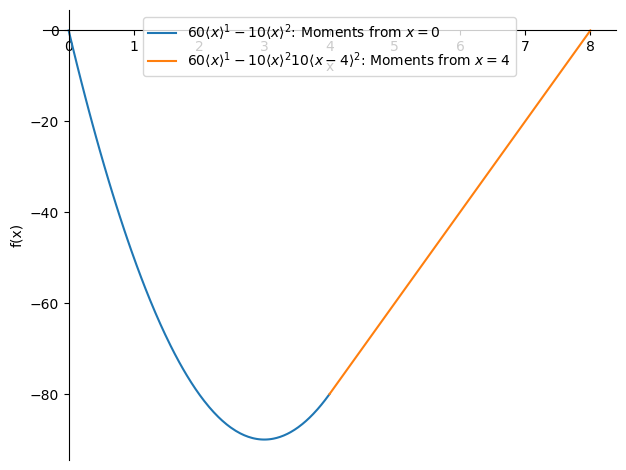
p0 = sp.plotting.plot(-M_subs.args[3]-M_subs.args[0],(x,0,4),label='$'+sp.latex(M_subs.args[3])+sp.latex(M_subs.args[0])+'$'+": Moments from $x = 0$",legend=True,show=False)
p2 = sp.plotting.plot(-M_subs.args[3]-M_subs.args[0]-M_subs.args[1],(x,4,8),label='$'+sp.latex(M_subs.args[3])+sp.latex(M_subs.args[0])+sp.latex(M_subs.args[1])+'$'+": Moments from $x = 4$",show=False)
p0.append(p2[0])
p0.show()

Displacements

The displacement is found by integrating and solving for with the boundary conditions:

kappa = M_sol / EI
phi = sp.integrate(kappa,x)+C1
display(phi)
w = -sp.integrate(phi,x) + C2
display(w)

\[\displaystyle C_{1} + \frac{\frac{3 q_{0} {\left\langle x \right\rangle}^{2}}{2} - \frac{q_{0} {\left\langle x \right\rangle}^{3}}{6} + \frac{q_{0} {\left\langle x - 4 \right\rangle}^{3}}{6} + \frac{q_{0} {\left\langle x - 8 \right\rangle}^{2}}{2}}{EI}\]

\[\displaystyle - C_{1} x + C_{2} - \frac{\frac{q_{0} {\left\langle x \right\rangle}^{3}}{2} - \frac{q_{0} {\left\langle x \right\rangle}^{4}}{24} + \frac{q_{0} {\left\langle x - 4 \right\rangle}^{4}}{24} + \frac{q_{0} {\left\langle x - 8 \right\rangle}^{3}}{6}}{EI}\]

eq3 = sp.Eq(w.subs(x,0),0)
display(eq3)
eq4 = sp.Eq(w.subs(x,8),0)
display(eq4)
sol = sp.solve((eq3,eq4),(C1,C2))
w_sol = w.subs(sol)
phi_sol = phi.subs(sol)
w_subs = w_sol.subs(((q0,20),(EI,10e-2 * 2e5)))
phi_subs = phi_sol.subs(((q0,20),(EI,10e-2 * 2e5)))
display(phi_subs)
display(sp.simplify(phi_subs.rewrite(sp.Piecewise)))
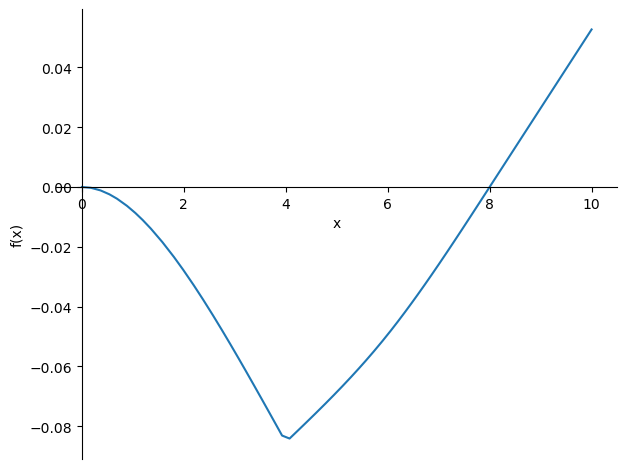
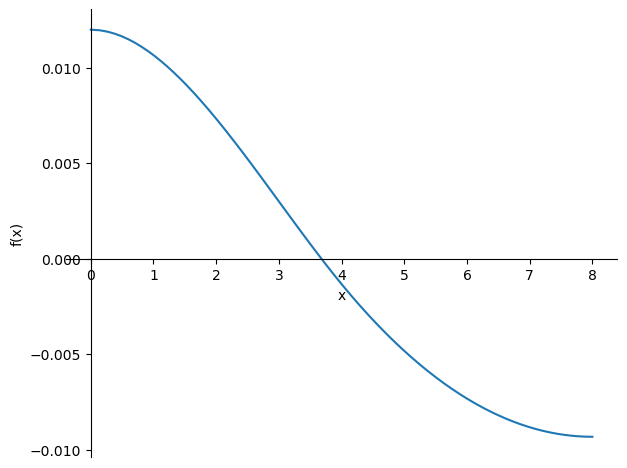
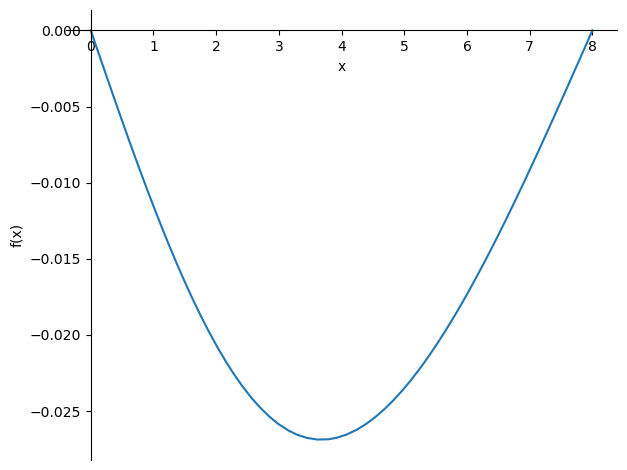
sp.plot(-phi_subs,(x,0,8))
display(w_subs)
display(sp.simplify(w_subs.rewrite(sp.Piecewise)))
sp.plot(-w_subs,(x,0,8));

\[\displaystyle C_{2} = 0\]

\[\displaystyle - 8 C_{1} + C_{2} - \frac{96 q_{0}}{EI} = 0\]

\[\displaystyle 0.0015 {\left\langle x \right\rangle}^{2} - 0.000166666666666667 {\left\langle x \right\rangle}^{3} + 0.000166666666666667 {\left\langle x - 4 \right\rangle}^{3} + 0.0005 {\left\langle x - 8 \right\rangle}^{2} - 0.012\]

\[\begin{split}\displaystyle \begin{cases} 0.00933333333333333 & \text{for}\: x > 8 \\- 0.0005 x^{2} + 0.008 x - 0.0226666666666667 & \text{for}\: x > 4 \\- 0.000166666666666667 x^{3} + 0.0015 x^{2} - 0.012 & \text{for}\: x > 0 \\-0.012 & \text{otherwise} \end{cases}\end{split}\]

\[\displaystyle 0.012 x - 0.0005 {\left\langle x \right\rangle}^{3} + 4.16666666666667 \cdot 10^{-5} {\left\langle x \right\rangle}^{4} - 4.16666666666667 \cdot 10^{-5} {\left\langle x - 4 \right\rangle}^{4} - 0.000166666666666667 {\left\langle x - 8 \right\rangle}^{3}\]

\[\begin{split}\displaystyle \begin{cases} 5.42101086242752 \cdot 10^{-20} x^{3} - 0.00933333333333333 x + 0.0746666666666667 & \text{for}\: x > 8 \\0.000166666666666667 x^{3} - 0.004 x^{2} + 0.0226666666666667 x - 0.0106666666666667 & \text{for}\: x > 4 \\x \left(4.16666666666667 \cdot 10^{-5} x^{3} - 0.0005 x^{2} + 0.012\right) & \text{for}\: x > 0 \\0.012 x & \text{otherwise} \end{cases}\end{split}\]

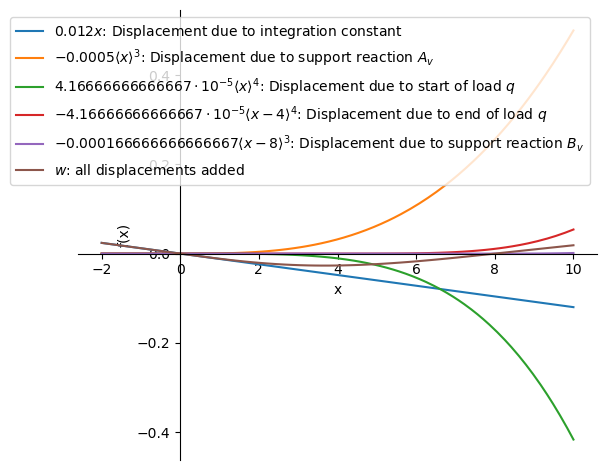
Again, the influence of the support reactions and load can be splitted:

p0 = sp.plotting.plot(-w_subs.args[1],(x,-2,10),label='$'+sp.latex(w_subs.args[1])+'$'+": Displacement due to integration constant",legend=True,show=False)
p1 = sp.plotting.plot(-w_subs.args[2],(x,-2,10),label='$'+sp.latex(w_subs.args[2])+'$'+": Displacement due to support reaction $A_v$",show=False)
p2 = sp.plotting.plot(-w_subs.args[0],(x,-2,10),label='$'+sp.latex(w_subs.args[0])+'$'+": Displacement due to start of load $q$",show=False)
p3 = sp.plotting.plot(-w_subs.args[3],(x,-2,10),label='$'+sp.latex(w_subs.args[3])+'$'+": Displacement due to end of load $q$",show=False)
p4 = sp.plotting.plot(-w_subs.args[4],(x,-2,10),label='$'+sp.latex(w_subs.args[4])+'$'+": Displacement due to support reaction $B_v$",show=False)
p5 = sp.plotting.plot(-w_subs,(x,-2,10),label='$w$: all displacements added',show=False)
p0.append(p1[0])
p0.append(p2[0])
p0.append(p3[0])
p0.append(p4[0])
p0.append(p5[0])
p0.show()

Hinged beam

Finding \(M\)- and \(V\)-line

As this is again a statically determinate structure, first the \(M\)- and \(V\)-line are solved for.

C1, C2, C3, C4, C5, x, EI = sp.symbols('C1, C2, C3, C4, C5, x, EI')
A_m, A_v, B_v = sp.symbols('A_m, A_v, B_v')
q0 = sp.symbols('q0')
F  = sp.symbols('F')

q = A_m * sp.SingularityFunction(x,0,-2) + A_v * sp.SingularityFunction(x,0,-1) + q0 *sp.SingularityFunction(x,0,0)- q0*sp.SingularityFunction(x,4,0) + F * sp.SingularityFunction(x,6,-1) + B_v * sp.SingularityFunction(x,8,-1)
display(q)

\[\displaystyle A_{m} {\left\langle x \right\rangle}^{-2} + A_{v} {\left\langle x \right\rangle}^{-1} + B_{v} {\left\langle x - 8 \right\rangle}^{-1} + F {\left\langle x - 6 \right\rangle}^{-1} + q_{0} {\left\langle x \right\rangle}^{0} - q_{0} {\left\langle x - 4 \right\rangle}^{0}\]

V1 = -sp.integrate(q,x)
display(V1)
M1 = sp.integrate(V1,x)
display(M1)

\[\displaystyle - A_{m} {\left\langle x \right\rangle}^{-1} - A_{v} {\left\langle x \right\rangle}^{0} - B_{v} {\left\langle x - 8 \right\rangle}^{0} - F {\left\langle x - 6 \right\rangle}^{0} - q_{0} {\left\langle x \right\rangle}^{1} + q_{0} {\left\langle x - 4 \right\rangle}^{1}\]

\[\displaystyle - A_{m} {\left\langle x \right\rangle}^{0} - A_{v} {\left\langle x \right\rangle}^{1} - B_{v} {\left\langle x - 8 \right\rangle}^{1} - F {\left\langle x - 6 \right\rangle}^{1} - \frac{q_{0} {\left\langle x \right\rangle}^{2}}{2} + \frac{q_{0} {\left\langle x - 4 \right\rangle}^{2}}{2}\]

Now the force and moment equilibria can be specified by substituting \(x=10\) for the equilibrium of the whole structure and \(x=4\) for the equilibrium of the structure up to the hinge.

eq1 = sp.Eq(V1.subs(x,10),0)
eq2 = sp.Eq(M1.subs(x,10),0)
eq3 = sp.Eq(M1.subs(x,4),0)
display(eq1)
display(eq2)
display(eq3)

\[\displaystyle - A_{v} - B_{v} - F - 4 q_{0} = 0\]

\[\displaystyle - A_{m} - 10 A_{v} - 2 B_{v} - 4 F - 32 q_{0} = 0\]

\[\displaystyle - A_{m} - 4 A_{v} - 8 q_{0} = 0\]

The three unknown support reactions can now be solved

sol = sp.solve((eq1,eq2,eq3),(A_m,A_v,B_v))
display(sol)

{A_m: 2*F + 8*q0, A_v: -F/2 - 4*q0, B_v: -F/2}

The \(M-\) and \(V-\)lines can now be found by subsituting our support reactions

M_sol = M1.subs(sol)
display(M_sol)
display(sp.simplify(M_sol.rewrite(sp.Piecewise)))
V_sol = V1.subs(sol)
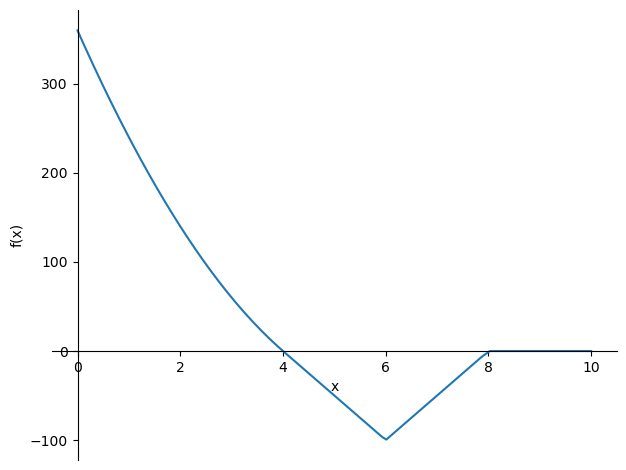
M_subs = M_sol.subs(((q0,20),(F,100)))
display(M_subs)
display(sp.simplify(M_subs.rewrite(sp.Piecewise)))
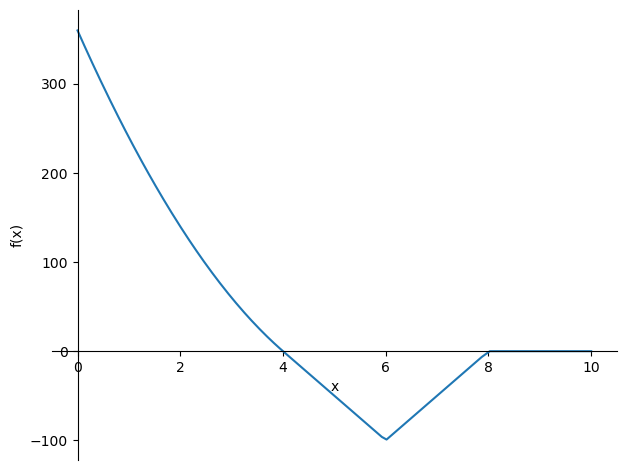
sp.plot(-M_subs,(x,0,10))
display(V_sol)
display(sp.simplify(V_sol.rewrite(sp.Piecewise)))
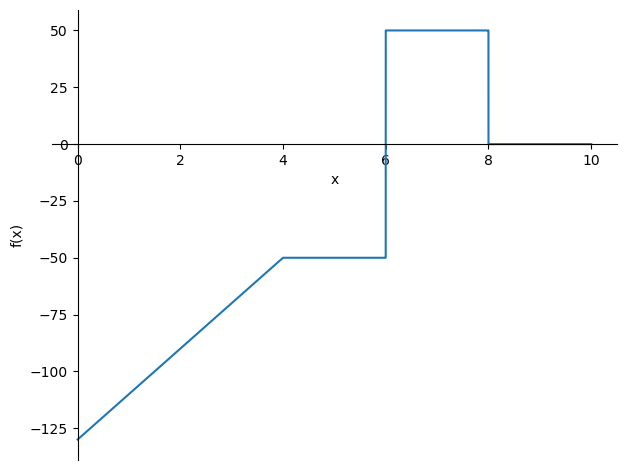
V_subs = V_sol.subs(((q0,20),(F,100)))
display(V_subs)
display(sp.simplify(V_subs.rewrite(sp.Piecewise)))
sp.plot(-V_subs,(x,0,10));

\[\displaystyle - F {\left\langle x - 6 \right\rangle}^{1} + \frac{F {\left\langle x - 8 \right\rangle}^{1}}{2} - \frac{q_{0} {\left\langle x \right\rangle}^{2}}{2} + \frac{q_{0} {\left\langle x - 4 \right\rangle}^{2}}{2} - \left(- \frac{F}{2} - 4 q_{0}\right) {\left\langle x \right\rangle}^{1} - \left(2 F + 8 q_{0}\right) {\left\langle x \right\rangle}^{0}\]

\[\begin{split}\displaystyle \begin{cases} 0 & \text{for}\: x > 8 \\\frac{F \left(8 - x\right)}{2} & \text{for}\: x > 6 \\\frac{F \left(x - 4\right)}{2} & \text{for}\: x > 4 \\- 2 F - \frac{q_{0} x^{2}}{2} - 8 q_{0} + \frac{x \left(F + 8 q_{0}\right)}{2} & \text{for}\: x > 0 \\0 & \text{otherwise} \end{cases}\end{split}\]

\[\displaystyle - 360 {\left\langle x \right\rangle}^{0} + 130 {\left\langle x \right\rangle}^{1} - 10 {\left\langle x \right\rangle}^{2} + 10 {\left\langle x - 4 \right\rangle}^{2} - 100 {\left\langle x - 6 \right\rangle}^{1} + 50 {\left\langle x - 8 \right\rangle}^{1}\]

\[\begin{split}\displaystyle \begin{cases} 0 & \text{for}\: x > 8 \\400 - 50 x & \text{for}\: x > 6 \\50 x - 200 & \text{for}\: x > 4 \\- 10 x^{2} + 130 x - 360 & \text{for}\: x > 0 \\0 & \text{otherwise} \end{cases}\end{split}\]

\[\displaystyle - F {\left\langle x - 6 \right\rangle}^{0} + \frac{F {\left\langle x - 8 \right\rangle}^{0}}{2} - q_{0} {\left\langle x \right\rangle}^{1} + q_{0} {\left\langle x - 4 \right\rangle}^{1} - \left(- \frac{F}{2} - 4 q_{0}\right) {\left\langle x \right\rangle}^{0} - \left(2 F + 8 q_{0}\right) {\left\langle x \right\rangle}^{-1}\]

\[\begin{split}\displaystyle \begin{cases} 0 & \text{for}\: x > 8 \\- \frac{F}{2} & \text{for}\: x > 6 \\\frac{F}{2} & \text{for}\: x > 4 \\\frac{F}{2} - q_{0} x + 4 q_{0} & \text{for}\: x > 0 \\\infty \left(- F - q_{0}\right) & \text{for}\: x = 0 \\0 & \text{otherwise} \end{cases}\end{split}\]

\[\displaystyle - 360 {\left\langle x \right\rangle}^{-1} + 130 {\left\langle x \right\rangle}^{0} - 20 {\left\langle x \right\rangle}^{1} + 20 {\left\langle x - 4 \right\rangle}^{1} - 100 {\left\langle x - 6 \right\rangle}^{0} + 50 {\left\langle x - 8 \right\rangle}^{0}\]

\[\begin{split}\displaystyle \begin{cases} -\infty & \text{for}\: x = 0 \\0 & \text{for}\: x > 8 \\-50 & \text{for}\: x > 6 \\50 & \text{for}\: x > 4 \\130 - 20 x & \text{for}\: x > 0 \\0 & \text{otherwise} \end{cases}\end{split}\]

C:\Users\tomvanwoudenbe\Anaconda3\lib\site-packages\sympy\plotting\plot.py:1618: RuntimeWarning: invalid value encountered in double_scalars
  cos_theta = dot_product / (vector_a_norm * vector_b_norm)

Finding \(W\)- and \(\phi\)-line

Now the displacement function is solved for. An unknown jump in the \(\phi\)-line (and consequently kink in the \(w\)-line) is added to account for the hinge.

kappa = M_sol.subs(sol) / EI
phi = sp.integrate(kappa,x)+C1 + C2*sp.SingularityFunction(x,4,0)
display(phi)
w = -sp.integrate(phi,x) + C3
display(w)

\[\displaystyle C_{1} + C_{2} {\left\langle x - 4 \right\rangle}^{0} + \frac{- 2 F {\left\langle x \right\rangle}^{1} + \frac{F {\left\langle x \right\rangle}^{2}}{4} - \frac{F {\left\langle x - 6 \right\rangle}^{2}}{2} + \frac{F {\left\langle x - 8 \right\rangle}^{2}}{4} - 8 q_{0} {\left\langle x \right\rangle}^{1} + 2 q_{0} {\left\langle x \right\rangle}^{2} - \frac{q_{0} {\left\langle x \right\rangle}^{3}}{6} + \frac{q_{0} {\left\langle x - 4 \right\rangle}^{3}}{6}}{EI}\]

\[\displaystyle - C_{1} x - C_{2} {\left\langle x - 4 \right\rangle}^{1} + C_{3} - \frac{- F {\left\langle x \right\rangle}^{2} + \frac{F {\left\langle x \right\rangle}^{3}}{12} - \frac{F {\left\langle x - 6 \right\rangle}^{3}}{6} + \frac{F {\left\langle x - 8 \right\rangle}^{3}}{12} - 4 q_{0} {\left\langle x \right\rangle}^{2} + \frac{2 q_{0} {\left\langle x \right\rangle}^{3}}{3} - \frac{q_{0} {\left\langle x \right\rangle}^{4}}{24} + \frac{q_{0} {\left\langle x - 4 \right\rangle}^{4}}{24}}{EI}\]

eq4 = sp.Eq(w.subs(x,0),0)
display(eq4)
eq5 = sp.Eq(phi.subs(x,0),0)
display(eq5)
eq6 = sp.Eq(w.subs(x,8),0)
display(eq6)
sol = sp.solve((eq4,eq5,eq6),(C1,C2,C3))
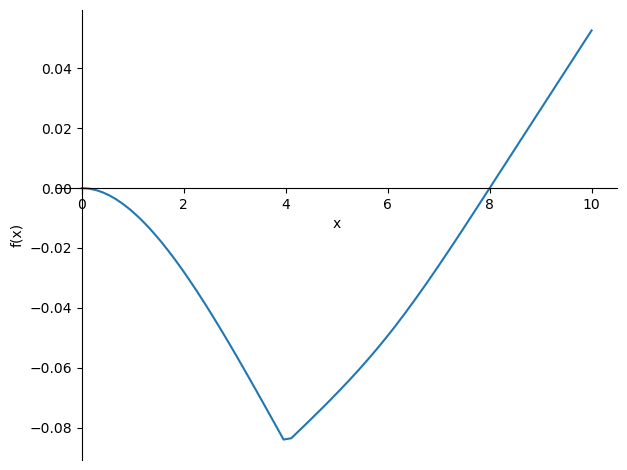
w_sol = w.subs(sol)
display(w_sol)
display(sp.simplify(w_subs.rewrite(sp.Piecewise)))
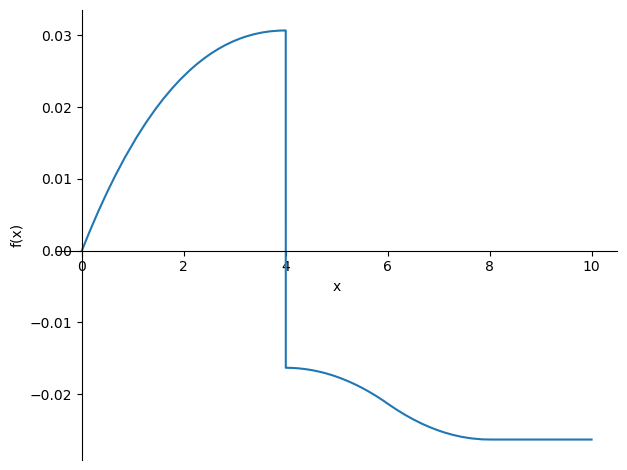
phi_sol = phi.subs(sol)
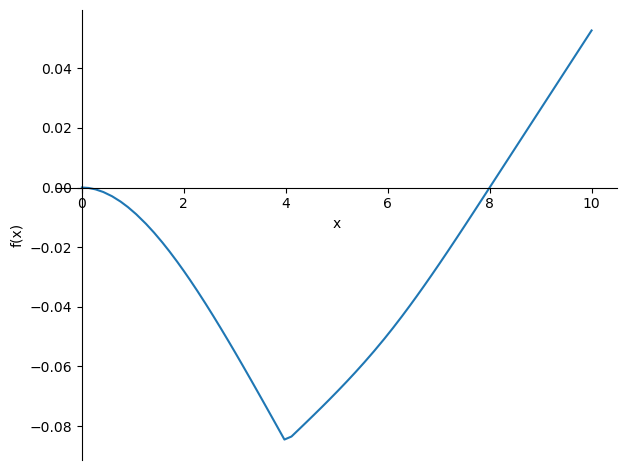
sp.plot(-phi_sol.subs(((q0,20),(F,100),(EI, 10e-2 * 2e5))),(x,0,10));
sp.plot(-w_sol.subs(((q0,20),(F,100),(EI, 10e-2 * 2e5))),(x,0,10));

\[\displaystyle C_{3} = 0\]

\[\displaystyle C_{1} = 0\]

\[\displaystyle - 8 C_{1} - 4 C_{2} + C_{3} - \frac{- \frac{68 F}{3} - \frac{224 q_{0}}{3}}{EI} = 0\]

\[\displaystyle - \frac{\left(17 F + 56 q_{0}\right) {\left\langle x - 4 \right\rangle}^{1}}{3 EI} - \frac{- F {\left\langle x \right\rangle}^{2} + \frac{F {\left\langle x \right\rangle}^{3}}{12} - \frac{F {\left\langle x - 6 \right\rangle}^{3}}{6} + \frac{F {\left\langle x - 8 \right\rangle}^{3}}{12} - 4 q_{0} {\left\langle x \right\rangle}^{2} + \frac{2 q_{0} {\left\langle x \right\rangle}^{3}}{3} - \frac{q_{0} {\left\langle x \right\rangle}^{4}}{24} + \frac{q_{0} {\left\langle x - 4 \right\rangle}^{4}}{24}}{EI}\]

\[\begin{split}\displaystyle \begin{cases} 5.42101086242752 \cdot 10^{-20} x^{3} - 0.00933333333333333 x + 0.0746666666666667 & \text{for}\: x > 8 \\0.000166666666666667 x^{3} - 0.004 x^{2} + 0.0226666666666667 x - 0.0106666666666667 & \text{for}\: x > 4 \\x \left(4.16666666666667 \cdot 10^{-5} x^{3} - 0.0005 x^{2} + 0.012\right) & \text{for}\: x > 0 \\0.012 x & \text{otherwise} \end{cases}\end{split}\]

Directly solving displacements

Now the same problem is solved directly for the displacements

q = A_m * sp.SingularityFunction(x,0,-2) + A_v * sp.SingularityFunction(x,0,-1) + 20 *sp.SingularityFunction(x,0,0)-20*sp.SingularityFunction(x,4,0) + 100 * sp.SingularityFunction(x,6,-1) + B_v * sp.SingularityFunction(x,8,-1)

V = -sp.integrate(q,x)
M = sp.integrate(V,x)

eq1 = sp.Eq(V.subs(x,10),0)
eq2 = sp.Eq(M.subs(x,10),0)
eq3 = sp.Eq(M.subs(x,4),0)
display(eq1)
display(eq2)
display(eq3)

\[\displaystyle - A_{v} - B_{v} - 180 = 0\]

\[\displaystyle - A_{m} - 10 A_{v} - 2 B_{v} - 1040 = 0\]

\[\displaystyle - A_{m} - 4 A_{v} - 160 = 0\]

kappa = M / EI
phi = sp.integrate(kappa,x) + C1 + C2*sp.SingularityFunction(x,4,0)
w = -sp.integrate(phi,x) + C3
display(w)

\[\displaystyle - C_{1} x - C_{2} {\left\langle x - 4 \right\rangle}^{1} + C_{3} - \frac{- \frac{A_{m} {\left\langle x \right\rangle}^{2}}{2} - \frac{A_{v} {\left\langle x \right\rangle}^{3}}{6} - \frac{B_{v} {\left\langle x - 8 \right\rangle}^{3}}{6} - \frac{5 {\left\langle x \right\rangle}^{4}}{6} + \frac{5 {\left\langle x - 4 \right\rangle}^{4}}{6} - \frac{50 {\left\langle x - 6 \right\rangle}^{3}}{3}}{EI}\]

eq4 = sp.Eq(w.subs(x,0),0)
display(eq4)
eq5 = sp.Eq(phi.subs(x,0),0)
display(eq5)
eq6 = sp.Eq(w.subs(x,8),0)
display(eq6)

\[\displaystyle C_{3} = 0\]

\[\displaystyle C_{1} = 0\]

\[\displaystyle - 8 C_{1} - 4 C_{2} + C_{3} - \frac{- 32 A_{m} - \frac{256 A_{v}}{3} - \frac{10000}{3}}{EI} = 0\]

sol = sp.solve((eq1,eq2,eq3,eq4,eq5,eq6),(C1,C2,C3,A_m,A_v,B_v))
display(sol)

{C1: 0, C2: 940/EI, C3: 0, A_m: 360, A_v: -130, B_v: -50}

M_sol = M.subs(sol)
display(sp.simplify(M_sol.rewrite(sp.Piecewise)))
display(M_sol)
sp.plot(-M_sol.subs(EI, 10e-2 * 2e5),(x,0,10))
w_sol = w.subs(sol)
display(w_sol)
display(sp.simplify(w_sol.rewrite(sp.Piecewise)))
sp.plot(-w_sol.subs(EI, 10e-2 * 2e5),(x,0,10));

\[\begin{split}\displaystyle \begin{cases} 0 & \text{for}\: x > 8 \\400 - 50 x & \text{for}\: x > 6 \\50 x - 200 & \text{for}\: x > 4 \\- 10 x^{2} + 130 x - 360 & \text{for}\: x > 0 \\0 & \text{otherwise} \end{cases}\end{split}\]

\[\displaystyle - 360 {\left\langle x \right\rangle}^{0} + 130 {\left\langle x \right\rangle}^{1} - 10 {\left\langle x \right\rangle}^{2} + 10 {\left\langle x - 4 \right\rangle}^{2} - 100 {\left\langle x - 6 \right\rangle}^{1} + 50 {\left\langle x - 8 \right\rangle}^{1}\]

\[\displaystyle - \frac{- 180 {\left\langle x \right\rangle}^{2} + \frac{65 {\left\langle x \right\rangle}^{3}}{3} - \frac{5 {\left\langle x \right\rangle}^{4}}{6} + \frac{5 {\left\langle x - 4 \right\rangle}^{4}}{6} - \frac{50 {\left\langle x - 6 \right\rangle}^{3}}{3} + \frac{25 {\left\langle x - 8 \right\rangle}^{3}}{3}}{EI} - \frac{940 {\left\langle x - 4 \right\rangle}^{1}}{EI}\]

\[\begin{split}\displaystyle \begin{cases} \frac{1580 \cdot \left(8 - x\right)}{3 EI} & \text{for}\: x > 8 \\\frac{5 \cdot \left(5 x^{3} - 120 x^{2} + 644 x - 32\right)}{3 EI} & \text{for}\: x > 6 \\\frac{5 \left(- 5 x^{3} + 60 x^{2} - 436 x + 2128\right)}{3 EI} & \text{for}\: x > 4 \\\frac{5 x^{2} \left(x^{2} - 26 x + 216\right)}{6 EI} & \text{for}\: x > 0 \\0 & \text{otherwise} \end{cases}\end{split}\]

Statically indeterminate structure

Now a statically indeterminate structure is solved,

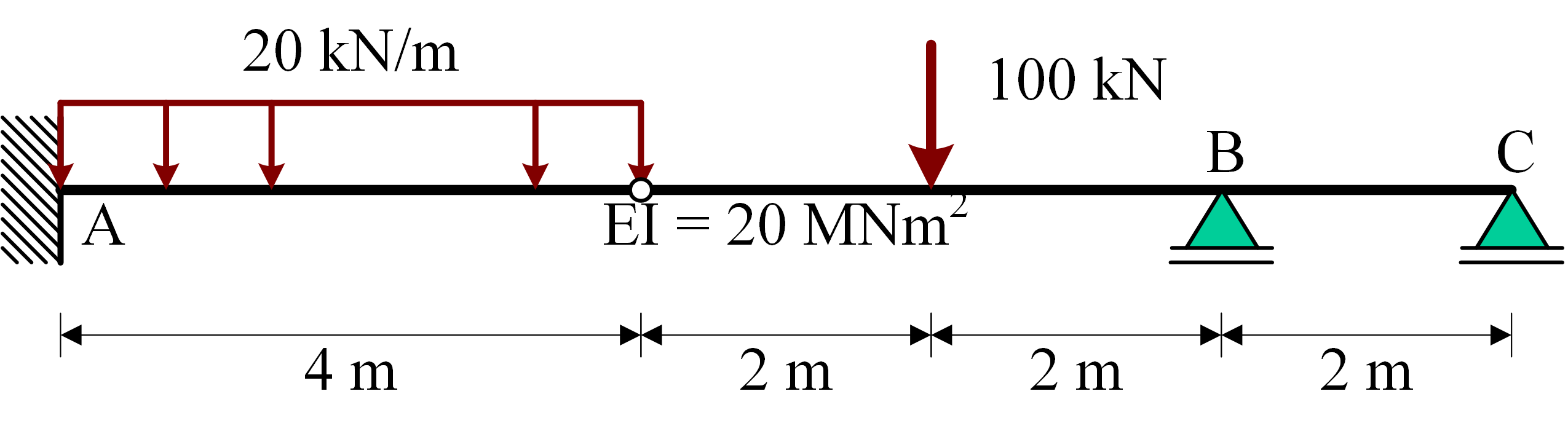
This adds one additional support reaction to be solved, but the additional equation is provided by \(w(10)=0\)

C_v = sp.symbols('C_v')
q = A_m * sp.SingularityFunction(x,0,-2) + A_v * sp.SingularityFunction(x,0,-1) + 20 *sp.SingularityFunction(x,0,0)-20*sp.SingularityFunction(x,4,0) + 100 * sp.SingularityFunction(x,6,-1) + B_v * sp.SingularityFunction(x,8,-1) + C_v * sp.SingularityFunction(x,10,-1)

V = -sp.integrate(q,x)
M = sp.integrate(V,x)

eq1 = sp.Eq(V.subs(x,10),0)
eq2 = sp.Eq(M.subs(x,10),0)
eq3 = sp.Eq(M.subs(x,4),0)
display(eq1)
display(eq2)
display(eq3)

\[\displaystyle - A_{v} - B_{v} - C_{v} - 180 = 0\]

\[\displaystyle - A_{m} - 10 A_{v} - 2 B_{v} - 1040 = 0\]

\[\displaystyle - A_{m} - 4 A_{v} - 160 = 0\]

kappa = M / EI
phi = sp.integrate(kappa,x) + C1 + C2*sp.SingularityFunction(x,4,0)
w = -sp.integrate(phi,x) + C3
display(w)

\[\displaystyle - C_{1} x - C_{2} {\left\langle x - 4 \right\rangle}^{1} + C_{3} - \frac{- \frac{A_{m} {\left\langle x \right\rangle}^{2}}{2} - \frac{A_{v} {\left\langle x \right\rangle}^{3}}{6} - \frac{B_{v} {\left\langle x - 8 \right\rangle}^{3}}{6} - \frac{C_{v} {\left\langle x - 10 \right\rangle}^{3}}{6} - \frac{5 {\left\langle x \right\rangle}^{4}}{6} + \frac{5 {\left\langle x - 4 \right\rangle}^{4}}{6} - \frac{50 {\left\langle x - 6 \right\rangle}^{3}}{3}}{EI}\]

eq4 = sp.Eq(w.subs(x,0),0)
display(eq4)
eq5 = sp.Eq(phi.subs(x,0),0)
display(eq5)
eq6 = sp.Eq(w.subs(x,8),0)
display(eq6)
eq7 = sp.Eq(w.subs(x,10),0)
display(eq7)

\[\displaystyle C_{3} = 0\]

\[\displaystyle C_{1} = 0\]

\[\displaystyle - 8 C_{1} - 4 C_{2} + C_{3} - \frac{- 32 A_{m} - \frac{256 A_{v}}{3} - \frac{10000}{3}}{EI} = 0\]

\[\displaystyle - 10 C_{1} - 6 C_{2} + C_{3} - \frac{- 50 A_{m} - \frac{500 A_{v}}{3} - \frac{4 B_{v}}{3} - 8320}{EI} = 0\]

sol = sp.solve((eq1,eq2,eq3,eq4,eq5,eq6,eq7),(C1,C2,C3,A_m,A_v,B_v,C_v))
display(sol)

{C1: 0, C2: 1556/(3*EI), C3: 0, A_m: 202, A_v: -181/2, B_v: -337/2, C_v: 79}

display(M.subs(sol))
display(sp.simplify(M.subs(sol).rewrite(sp.Piecewise)))
sp.plot(-M.subs(sol),(x,0,10))
display(V.subs(sol))
display(sp.simplify(V.subs(sol).rewrite(sp.Piecewise)))
sp.plot(-V.subs(sol),(x,0,10))
display(w_sol.subs(sol))
display(sp.simplify(w_sol.subs(sol).rewrite(sp.Piecewise)))
sp.plot(-w_sol.subs(EI,10e-2 * 2e5).subs(sol),(x,0,10));

\[\displaystyle - 202 {\left\langle x \right\rangle}^{0} + \frac{181 {\left\langle x \right\rangle}^{1}}{2} - 10 {\left\langle x \right\rangle}^{2} + 10 {\left\langle x - 4 \right\rangle}^{2} - 100 {\left\langle x - 6 \right\rangle}^{1} + \frac{337 {\left\langle x - 8 \right\rangle}^{1}}{2} - 79 {\left\langle x - 10 \right\rangle}^{1}\]

\[\begin{split}\displaystyle \begin{cases} 0 & \text{for}\: x > 10 \\79 x - 790 & \text{for}\: x > 8 \\558 - \frac{179 x}{2} & \text{for}\: x > 6 \\\frac{21 x}{2} - 42 & \text{for}\: x > 4 \\- 10 x^{2} + \frac{181 x}{2} - 202 & \text{for}\: x > 0 \\0 & \text{otherwise} \end{cases}\end{split}\]

\[\displaystyle - 202 {\left\langle x \right\rangle}^{-1} + \frac{181 {\left\langle x \right\rangle}^{0}}{2} - 20 {\left\langle x \right\rangle}^{1} + 20 {\left\langle x - 4 \right\rangle}^{1} - 100 {\left\langle x - 6 \right\rangle}^{0} + \frac{337 {\left\langle x - 8 \right\rangle}^{0}}{2} - 79 {\left\langle x - 10 \right\rangle}^{0}\]

\[\begin{split}\displaystyle \begin{cases} -\infty & \text{for}\: x = 0 \\0 & \text{for}\: x > 10 \\79 & \text{for}\: x > 8 \\- \frac{179}{2} & \text{for}\: x > 6 \\\frac{21}{2} & \text{for}\: x > 4 \\\frac{181}{2} - 20 x & \text{for}\: x > 0 \\0 & \text{otherwise} \end{cases}\end{split}\]

\[\displaystyle - \frac{- 180 {\left\langle x \right\rangle}^{2} + \frac{65 {\left\langle x \right\rangle}^{3}}{3} - \frac{5 {\left\langle x \right\rangle}^{4}}{6} + \frac{5 {\left\langle x - 4 \right\rangle}^{4}}{6} - \frac{50 {\left\langle x - 6 \right\rangle}^{3}}{3} + \frac{25 {\left\langle x - 8 \right\rangle}^{3}}{3}}{EI} - \frac{940 {\left\langle x - 4 \right\rangle}^{1}}{EI}\]

\[\begin{split}\displaystyle \begin{cases} \frac{1580 \cdot \left(8 - x\right)}{3 EI} & \text{for}\: x > 8 \\\frac{5 \cdot \left(5 x^{3} - 120 x^{2} + 644 x - 32\right)}{3 EI} & \text{for}\: x > 6 \\\frac{5 \left(- 5 x^{3} + 60 x^{2} - 436 x + 2128\right)}{3 EI} & \text{for}\: x > 4 \\\frac{5 x^{2} \left(x^{2} - 26 x + 216\right)}{6 EI} & \text{for}\: x > 0 \\0 & \text{otherwise} \end{cases}\end{split}\]