CIE_4140_Lecture_18_Part_1_Python

Excitation of a rod by a point pulse-load \(P_0 Dirac(x) Dirac(t)\)

import sympy as sp

u = sp.symbols('u',cls=sp.Function)
x, k= sp.symbols('x, k',real=True)
t = sp.symbols('t',real=True)
c, P_0 = sp.symbols('c P_0')

EM = sp.diff(u(x,t),t,2)-c**2*sp.diff(u(x,t),x,2)-P_0 * sp.DiracDelta(x)*sp.DiracDelta(t)
display(EM)

\[\displaystyle - P_{0} \delta\left(t\right) \delta\left(x\right) - c^{2} \frac{\partial^{2}}{\partial x^{2}} u{\left(x,t \right)} + \frac{\partial^{2}}{\partial t^{2}} u{\left(x,t \right)}\]

EM_fourier = sp.fourier_transform(EM,x,k)
display(EM_fourier)

\[\displaystyle - P_{0} \delta\left(t\right) - c^{2} \mathcal{F}_{x}\left[\frac{\partial^{2}}{\partial x^{2}} u{\left(x,t \right)}\right]\left(k\right) + \mathcal{F}_{x}\left[\frac{\partial^{2}}{\partial t^{2}} u{\left(x,t \right)}\right]\left(k\right)\]

U = sp.symbols('U',cls=sp.Function)
EM_fourier = EM_fourier.subs(sp.FourierTransform(sp.Derivative(u(x, t), (x, 2)), x, k),-k**2*U(t))
EM_fourier = EM_fourier.subs(sp.FourierTransform(sp.Derivative(u(x, t), (t, 2)), x, k),sp.Derivative(U(t), (t, 2)))
display(EM_fourier)
print(EM_fourier)

\[\displaystyle - P_{0} \delta\left(t\right) + c^{2} k^{2} U{\left(t \right)} + \frac{d^{2}}{d t^{2}} U{\left(t \right)}\]

-P_0*DiracDelta(t) + c**2*k**2*U(t) + Derivative(U(t), (t, 2))

C1, C2 = sp.symbols('C1, C2')
Solution_fourier = sp.dsolve(EM_fourier,U(t)).rhs
display(Solution_fourier)

\[\displaystyle \left(C_{1} - \frac{i P_{0} \theta\left(t\right)}{2 c k}\right) e^{i c k t} + \left(C_{2} + \frac{i P_{0} \theta\left(t\right)}{2 c k}\right) e^{- i c k t}\]

Solution_fourier = sp.simplify(Solution_fourier.subs([(C1,0),(C2,0)]))
display(Solution_fourier)
Solution_fourier_sub = Solution_fourier.subs([(P_0,1),(c,1)])
display(Solution_fourier_sub)

\[\displaystyle \frac{P_{0} \sin{\left(c k t \right)} \theta\left(t\right)}{c k}\]

\[\displaystyle \frac{\sin{\left(k t \right)} \theta\left(t\right)}{k}\]

Solution = sp.integrate(Solution_fourier_sub*sp.cos(k*x),(k,0,1e20))/sp.pi
display(Solution)

\[\displaystyle \frac{\frac{\theta\left(t\right) \operatorname{Si}{\left(1.0 \cdot 10^{20} t - 1.0 \cdot 10^{20} x \right)}}{2} + \frac{\theta\left(t\right) \operatorname{Si}{\left(1.0 \cdot 10^{20} t + 1.0 \cdot 10^{20} x \right)}}{2}}{\pi}\]

Result not fully correct, so an arbitrary high value is given, Maple gives limit of k to infinity

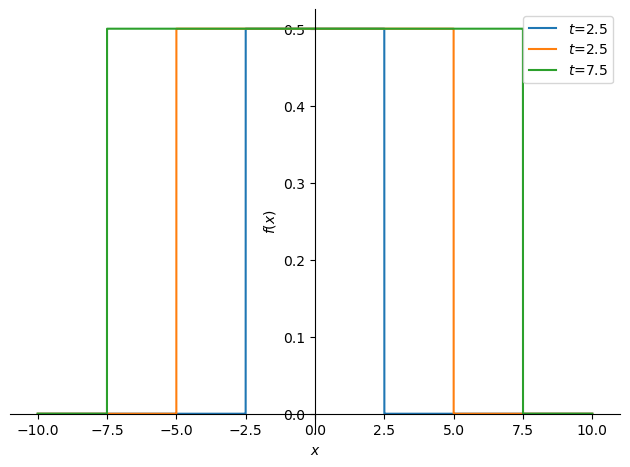
p0 = sp.plotting.plot(Solution.subs(t,2.5),(x,-10,10),label='$t$=2.5' ,legend=True,show=False)
p1 = sp.plotting.plot(Solution.subs(t,5),(x,-10,10),label='$t$=2.5' ,show=False)
p2 = sp.plotting.plot(Solution.subs(t,7.5),(x,-10,10),label='$t$=7.5' ,show=False)
p0.append(p1[0])
p0.append(p2[0])
p0.show()

Excitation of a rod on elastic foundation by a point pulse-load \(P_0 DiracDelta(x) DiracDelta(t)\)

u = sp.symbols('u',cls=sp.Function)
x, k= sp.symbols('x, k',real=True)
t = sp.symbols('t',real=True)
c, P_0,omega_0 = sp.symbols('c P_0 omega_0')

EM = sp.diff(u(x,t),t,2)-c**2*sp.diff(u(x,t),x,2)+omega_0**2*u(x,t)-P_0*sp.DiracDelta(x)*sp.DiracDelta(t)
display(EM)

\[\displaystyle - P_{0} \delta\left(t\right) \delta\left(x\right) - c^{2} \frac{\partial^{2}}{\partial x^{2}} u{\left(x,t \right)} + \omega_{0}^{2} u{\left(x,t \right)} + \frac{\partial^{2}}{\partial t^{2}} u{\left(x,t \right)}\]

EM_fourier = sp.fourier_transform(EM,x,k)
display(EM_fourier)

\[\displaystyle - P_{0} \delta\left(t\right) - c^{2} \mathcal{F}_{x}\left[\frac{\partial^{2}}{\partial x^{2}} u{\left(x,t \right)}\right]\left(k\right) + \omega_{0}^{2} \mathcal{F}_{x}\left[u{\left(x,t \right)}\right]\left(k\right) + \mathcal{F}_{x}\left[\frac{\partial^{2}}{\partial t^{2}} u{\left(x,t \right)}\right]\left(k\right)\]

U = sp.symbols('U',cls=sp.Function)
EM_fourier = EM_fourier.subs(sp.FourierTransform(u(x, t),x,k),U(t))
EM_fourier = EM_fourier.subs(sp.FourierTransform(sp.Derivative(u(x, t), (x, 2)), x, k),-k**2*U(t))
EM_fourier = EM_fourier.subs(sp.FourierTransform(sp.Derivative(u(x, t), (t, 2)), x, k),sp.Derivative(U(t), (t, 2)))
display(EM_fourier)

\[\displaystyle - P_{0} \delta\left(t\right) + c^{2} k^{2} U{\left(t \right)} + \omega_{0}^{2} U{\left(t \right)} + \frac{d^{2}}{d t^{2}} U{\left(t \right)}\]

C1, C2 = sp.symbols('C1, C2')
Solution_fourier = sp.dsolve(EM_fourier,U(t)).rhs
display(Solution_fourier)

\[\displaystyle \left(C_{1} - \frac{P_{0} \theta\left(t\right)}{2 \sqrt{- c^{2} k^{2} - \omega_{0}^{2}}}\right) e^{- t \sqrt{- c^{2} k^{2} - \omega_{0}^{2}}} + \left(C_{2} + \frac{P_{0} \theta\left(t\right)}{2 \sqrt{- c^{2} k^{2} - \omega_{0}^{2}}}\right) e^{t \sqrt{- c^{2} k^{2} - \omega_{0}^{2}}}\]

Solution_fourier = sp.simplify(Solution_fourier.subs([(C1,0),(C2,0)]))
display(Solution_fourier)
Solution_fourier_sub = Solution_fourier.subs([(P_0,1),(c,1),(omega_0,sp.sqrt(2))])
display(Solution_fourier_sub)

\[\displaystyle \frac{P_{0} \sinh{\left(t \sqrt{- c^{2} k^{2} - \omega_{0}^{2}} \right)} \theta\left(t\right)}{\sqrt{- c^{2} k^{2} - \omega_{0}^{2}}}\]

\[\displaystyle \frac{\sinh{\left(t \sqrt{- k^{2} - 2} \right)} \theta\left(t\right)}{\sqrt{- k^{2} - 2}}\]

Solution = sp.integrate(Solution_fourier_sub*sp.cos(k*x),(k,0,sp.oo))/sp.pi
display(Solution)

\[\displaystyle - \frac{i \left(\int\limits_{0}^{\infty} \left(- \frac{e^{- t \sqrt{- k^{2} - 2}} \cos{\left(k x \right)}}{\sqrt{k^{2} + 2}}\right)\, dk + \int\limits_{0}^{\infty} \frac{e^{t \sqrt{- k^{2} - 2}} \cos{\left(k x \right)}}{\sqrt{k^{2} + 2}}\, dk\right) \theta\left(t\right)}{2 \pi}\]

Werkt ook niet in Maple

Solution = sp.Heaviside(t)/2*sp.besselj(0,sp.sqrt(2)*sp.sqrt(t**2-x**2))*sp.Heaviside(t**2-x**2)
display(Solution)

\[\displaystyle \frac{\theta\left(t\right) \theta\left(t^{2} - x^{2}\right) J_{0}\left(\sqrt{2} \sqrt{t^{2} - x^{2}}\right)}{2}\]

%matplotlib notebook

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

Solution_func = sp.lambdify((x,t),Solution)

fig, ax = plt.subplots()
xdata = np.linspace(-5,5,100)
line, = ax.plot([], [])
ax.set_xlim(-5,5)
ax.set_ylim(-0.2,0.5)

def update(frame):
    ydata = Solution_func(x=xdata,t=frame)
    ax.set_title("Displacement versus x for $t$ = "+str(np.round(frame,2)))
    line.set_data(xdata, ydata)

ani = FuncAnimation(fig, update, frames=np.linspace(0,4.9,100),interval = 100)
plt.show()